пока только решение к заданию 327.
остальное решу и допишу
рис 231.
прямые m,n параллельны,т.к. соответвенные углы равны(по 100 град.); угол,смежный со вторым является соответственным углу 94 град.; значит угол 2+94=180град. угол2=180-94=86 град.
Объяснение:
Задание 330 рисунок к нему ниже
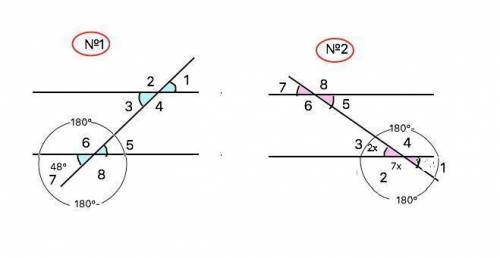
1) меньшие по 48°, большие по 132°.
2) меньшие по 40°, большие по 140°
При пересечении двух параллельных прямых секущей образуется пары равных углов:
соответственные (2 и 6, 1 и 5, 3 и 7, 4 и 8).
накрестлежащие: (3 и 5, 4 и 6 - внутренние ), (2 и 8, 1 и 7 - внешние). кроме того, равны и пары вертикальных углов.
1) Как известно, сумма смежных углов равна 180°. Поэтому углы, смежные углу, равному 48°, равны 180°-48°=132°
На рисунке 1 все мéньшие углы, окрашенные голубым, равны 48°. все бóльшие - 132°
2) На рисунке 2 смежные углы 2 и 3 относятся как 2:7. Т.е. развернутый угол делится на 2+7=9 частей. Каждая часть равна 180°:9=20°. Поэтому все мéньшие углы равны 2•20°=40°, бóльшие 7•20°=140°.
Задание 329
а ‖ b, с - секущая.
∟1 i ∟2 внутренние односторонние. ∟1> ∟2 в 4 раза.
Найти: ∟1; ∟2.
Пусть ∟2 = х; тогда ∟1 = 4х. Если а ‖ b, с - секущая,
тогда по признаку параллельности прямых имеем:
∟1 + ∟2 = 180 °.
Составим i решим уравнение:
4х + х = 180; 5х = 180; х = 180: 5;
х = 36 ∟2 = 36 °; ∟1 = 4 • 36 ° = 144 °
ответ. 36 ° и 144 °
Найдите углы A и B треугольника ABC, если AB=12 см, BC=6√6 см, угол C= 45°.
ответ: 60° , 75° или 120° , 15° .
Объяснение:
По теореме синусов : BC / sin(∠A) =AB / sin(∠C ) ⇔
6√6/sin(∠A)=12/sin45°⇔sin(∠A) =6√6*sin45°/12=6√6 *(√2/2) / 12 = 3 /2 ⇒
∠A= 60° или ∠A= 120° . Оба верны ∠A > ∠C , т.к. BC > AB
( в треугольнике против большой стороны лежит большой угол )
* * * BC > AB : BC = 6√6 > 6√4 = 12 = AB * * *
∠B = 180° - (∠A+√C) → ∠B = 75° или ∠B = 15° см. лишнее приложение