S полной поверхности параллелепипеда = 2 S основания + 4 S боковой грани
S основания = S ромба =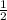
* на произведение диагоналей, одна диагональ = стороне. образовывает треугольник с углами 60 град. (формула для решения)
это равносторонний треугольник
2 диагональ из равностороннего треугольника со стороной a, и высотой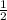 a и углом в вершине 120 град. В нем: прямоугольный треугольник с сторонами 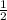*a (половина 1 диагонали), гипотенуза = a.
По т.пифагора: (корень из 3)*a/2
2 диагональ (равна корень из 3)*a
площадь основания = (корень из 3)*a*a/2.
найдем высоту. 45 град. угол между диагональю параллелепипеда и 2 диагональю ромба.
в треугольнике, образованном диагональю параллелепипеда диагональю ромба и боковой стороной параллелепипед один угол 45 град, второй = 90 град, то третий будет 180 - 45 - 90.
данный треугольник - равносторонний и высота равна диагонали ромба т.е. (корень из 3)*a. (в следствии)
Следовательно площадь боковой грани = a*(корень из 3)*a
Итого П.П.П. = 2*(корень из 3)*a*a/2 + 4*a*(корень из 3)*a = 5*(корень из 3)*(a в квадрате) (формулой)
Объяснение:
r - радиус вписанной окружности, r = 12 см.
АВ = NP = 2r = 2 x 12 = 24 см.
СН - высота трапеции, СН = АВ = 24 см.
По теореме Пифагора в треугольнике НСD:
CD^2 = CH^2 + HD^2;
25^2 = 24^2 + HD^2;
625 = 576 + HD^2;
HD^2 = 49;
HD = 7 см.
Пусть NC = x см. Тогда по свойству касательных СК = NC = х см.
DK = DC - CK = 25 - x.
PH = NC = x;
DP = DH + PH = 7 + x.
По свойству касательных: DP = DК. Получим уравнение:
7 + х = 25 - х;
х + х = 25 - 7;
2х = 18;
х = 9.
NC = 9 см;
ВС = BN + NC = r + x = 12 + 9 = 21 см;
AD = AP + PD = r + 7 + x = 12 + 7 + 9 = 28 см.
Периметр трапеции:
P = AB + BC + CD + AD = 24 + 21 + 25 + 28 = 98 см.
88 см².
Объяснение:
Будем считать, что в условии описка, что "площадь треугольника ABD - 60 см“.
1) Пусть BH - высота треугольника DBA, тогда по теореме
S ∆ = 1/2•AD•BH
60 = 1/2•15•BH
120 = 15•BH
ВH = 120 : 15
BH = 8 см.
2) Высота треугольника является и высотой трапеции, т.к. длина ВН - это расстояние между параллельными основаниями трапеции.
S трапеции = (a+b)•h / 2
В нашем случае
S трапеции = (АD+BC)•BH / 2 = (15+7)•8/2 = 22•4 = 88 (см²).