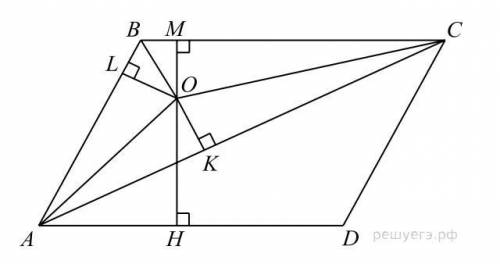
Насколько мне помнится, то тут нужно решать объяснениями, если да то: Пусть O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём
Отрезки и OK равны как радиусы вписанной в треугольник ABC окружности, то есть Рассмотрим треугольники ALO и AOK, они прямоугольные, углы LAO и OAK равны, AO — общая, следовательно, треугольники равны, откуда Аналогично из равенства треугольников COM и COK получаем а из равенства треугольников BOL и BOM — Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:
Площадь параллелограмма равна произведению высоты на основание:
Рассмотрим треугольники ABC и ACD, AB равно CD, AD равно BC, углы ABC и ADC равны, следовательно, треугольники ABC и ACD равны. Поэтому площадь треугольника ABC равна половине площади параллелограмма т.е 168
Запишите уравнение прямой, которая проходит через точки Ки L, если точка K- середина отрезка MN. Координаты точек: L(3;5), M(1;-2), N(-1;0).
Объяснение:
1) K- середина отрезка MN , M(1;-2), N(-1;0).
х(К)= ( х(M)+х(N) )/2 , х(К)= ( 1-1 )/2 , х(К)= 0 ;
у(К)= ( у(M)+у(N) )/2 , у(К)= ( -2+0 )/2 , у(К)=-1
К( 0 ; -1).
2) у=кх+в уравнение прямой
К( 0 ; -1) : -1=к*0+в ⇒ в=-1.
L( 3; 5) : 5=к*3-1 ⇒ к=2.
у=2х-1.