ответ: S= 420
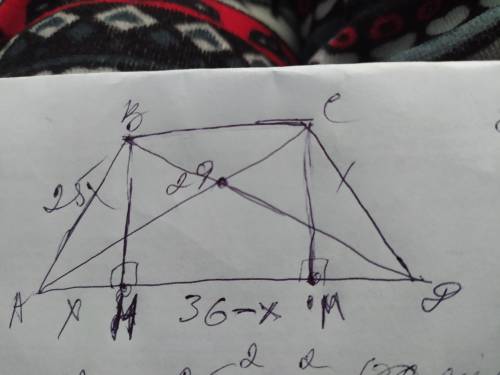
Объяснение: Проведём от вершины В высоту ВН. К нам получилось 2 прямоугольных треугольника АВН и ВДН. Пусть отрезок АН=х, тогда отрезок ДН=36-х. Высота ВН является общей стороной этих треугольников. Составим уравнение по теореме Пифагора:
25^-х^=29^-(36-х)^
625-х^=841-(1296-72х+х^)
625-х^=841-1296+72х-х^
-х^+х^-72х=841-1296-625
-72х= - 1080
х= - 1080÷(-72)
х=20
Мы нашли высоту ВН =20.
Теперь найдём ВС - верхнее основание.
Проведём ещё одну высоту СМ от вершины С к нижнему основанию трапеции. Две высоты отсекают он нижнего основания отрезок равный верхнему основанию:
ВС=НМ=36-2×15=36-30=6; ВС=НМ=6
Теперь найдём площадь трапеции:
S=1/2(АД+ВС)×ВН:
(36+6)÷2×20=42÷2×20=21×20=420
Поскольку отрезок DE (параллельный плоскости альфа) лежит в плоскости треугольника АВС, а плоскость треугольника АВС пересекает плоскость альфа по прямой ВС, значит, линия пересечения плоскостей (линия ВС) параллельна DE. Т.е. DE и ВС параллельны. Отсюда следует, что треугольники АВС и АДЕ – подобны, т.к. отрезок, параллельный стороне треугольника, отсекает треугольник подобный данному. АВ = АД + ДВ = 9 + 2 = 11 условных единиц. Из подобия указанных треугольников можно записать ВС/ДЕ = АВ/АД. Отсюда ВС= АВ*ДЕ/АД = 11*7/9 =77/9 см.