Площадь круга, как Вы помните, находят по формуле
S=πr²
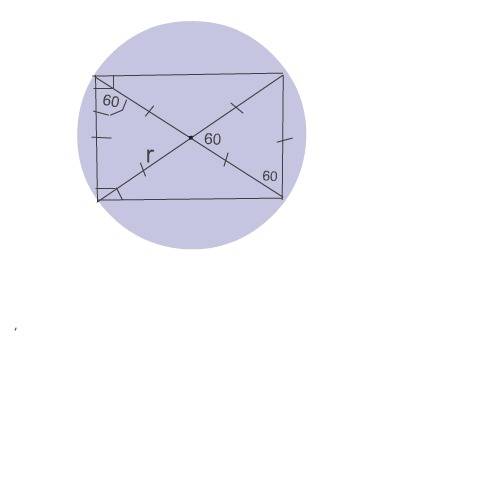
Радиус находим из остроугольных треугольников, образовавшимися диагоналями при меньшей стороне прямоугольника.
Эти треугольники - равносторонние, т.к. угол при пересечении диагоналей равен 60°, а сами диагонали делятся пополам и этим образуют равнобедренные треугольники, углы которых при основании, равном меньшей стороне вписанного прямоугольника, тоже равны 60°.⇒cледовательно, каждая половина диагонали равна меньшей стороне прямоугольника. А так как диагонали здесь являются диаметрами окружности, то радиус описанного круга тоже равен меньшей стороне прямоугольника.
r=10 см
S=πr²,
S=100 π см²
x^2-10x+12=0
По теореме Виета:
x1+x2=10
x1*x2=12
Преобразуем выражение, которе надо найти:
x2/x1 +x1/x2=((x1)^2+(x2)^2)/(x1*x2) (*)
Если x1+x2=10,то возведя обе части этого уравнения в квадрат, получим:
(x1)^2+2*(x1x2)+(x2)^2=100
(x1)^2+(x2)^2=100-2*(x1x2)=100-2*12=100-24=76
Подставим в (*) и получим
((x1)^2+(x2)^2)/(x1*x2)=76/12=19/3