
Объяснение:
Прямоугольник АВСD
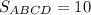
BE = EF = FC
AG = GD
-------------------------

-------------------------
Пусть длинные стороны прямоугольника равны а, а короткие - b.
ВС = AD = a
FD = СВ = b
Тогда площадь прямоугольника
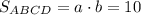
ΔBEH ~ ΔDGH по двум углам (∠BEH = ∠DHG - вертикальные углы; ∠HBE = ∠HDG -внутренние накрест лежащие углы при ВС║AD и секущей BD)
Из подобия этих треугольников следует пропорциональность сторон BE = a/3 и DG = a/2, откуда , что коэффициент подобия
k = a/3 : a/2 = 2/3
Высоты этих треугольников также относятся как 2:3, и высота ΔDGH равна 3b/5. Площадь ΔDGH равна
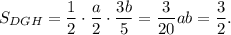
ΔBFK ~ ΔDGK по двум углам (∠BKFH = ∠DKG - вертикальные углы; ∠KBF = ∠KDG -внутренние накрест лежащие углы при ВС║AD и секущей BD) .
Из подобия этих треугольников следует пропорциональность сторон BF = 2a/3 и DG = a/2, откуда коэффициент подобия
k = 2/3 : a/2 = 4/3
Высоты этих треугольников также относятся как 4:3, и высота ΔDGK равна 3b/7. Площадь ΔDGK равна
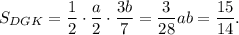
Площадь ΔGHK
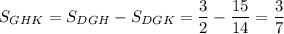
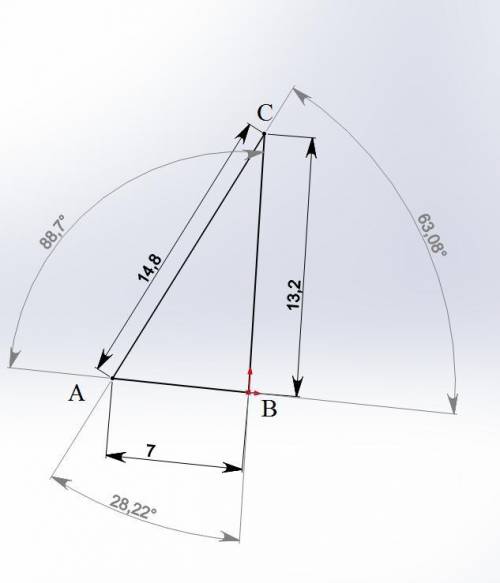
а) ∠С=30°; а=19,3 см; в=14,1 см
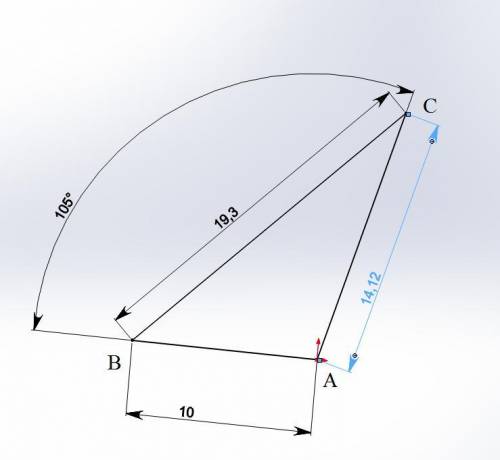
б) в=5,65 см; ∠А=17,35°; ∠С=118,1°
с) ∠А=63,08°; ∠В=88,7°; ∠С=28,22°
Объяснение:
а) ∠А=105°; ∠В=45°; с=10 см
∠С, а, в ?
∠С=180°-105°-45°=30°
а/sin∠А=с/sin∠С=10/sin30°=20
а=20*sin∠А=20*sin105°=19,3 см
в=20*sin∠В=20*sin45°=14,1 см
б) с=7,1 см ; а=2,4 см ; ∠В=44°33'
в, ∠А, ∠С ?
в²= а²+с²-2а*с*cos∠В=2,4²+7,1²-2*2,4*7,1*cos44°33'=31,9
в=5,65 см
sin∠А=sin∠В/в*а=sin44°33'/5,65*2,4=0,3
∠А=17,35°
sin∠С=sin∠В/в*с=sin44°33'/5,65*7,1=0,88
∠С=118,1°
с) а=13,2 см ; в=14,8 см; с=7см
а²=в²+с²-2*в*с*cos∠А
13,2²=14,8²+7²-2*14,8*7*cos∠А
cos∠А=93,8/207,2=0,45;
∠А=63,08°;
sin∠В=sin∠А/а*в=sin63,08°/13,2*14,8=0,9997
∠В=88,7°
sin∠С=sin∠А/а*с=sin63,08°/13,2*7=0,7=0,47
∠С=28,22°
Площадь прямоугольника находят умножением длин сторон:
х*2х=72
2х²=72
х²=36
х=6 см
2х=12 см
Периметр прямоугольника есть сумма длин всех сторон:
6+6+12+12=36 см
или иначе
2(6+12)=36 см