ответ: 432π
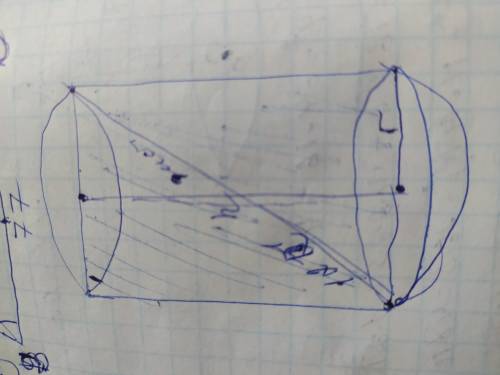
Объяснение: обозначим радиус r, a высоту h. Если r/h=1/2, то: h=2r. 2 радиуса
- это диаметр, и диаметр основания равен высоте. Высота, радиус и диагональ осевого сечения цилиндра образуют равнобедренный прямоугольный треугольник, в котором диаметр основания и высота являются катетами а диагональ гипотенузой. В равнобедренном прямоугольном треугольнике гипотенуза больше катета в √2 раз, поэтому h=диаметру=12√2/√2=
=12, тогда радиус=12/2=6
Найдём площадь основания по формуле:
Sосн=πr²=π×6²=36π
Теперь найдём объем цилиндра зная его площадь основания и высоту по формуле: V=Sосн×h=36π×12=432π(ед³)
25
Объяснение:
Биссектрисы углов пересекаются под прямым углом. Получается прямоугольный треугольник. Известно два катета, нужно найти гипотенузу. По теореме Пифагора:
а(в квадрате) + в(в квадрате)=с(в квадрате)
15(в квадрате)+20(в квадрате)=с(в квадрате)
225+400=с(в квадрате)
с(в квадрате)=625
с=25