1) 30°;
2) 12 см;
3) 6 см.
Объяснение:
В ∆ MKP ∠K = 60°, ∠P = 90°, тогдп
1) ∠M = 180° - (60° + 90°) = 30°.
2) РК - катет, лежащий напротив угла в 30°, тогда по теореме он равен половине гипотенузы МК, получим
РК = 1/2 • МК = 1/2•24 = 12 (см)
3) РК - катет, лежащий напротив угла в 30°, тогда по теореме он равен половине гипотенузы МК, получим
МК = 2•РК = 2•30 мм = 60 мм = 6 см.
81√3 ед²
Объяснение:
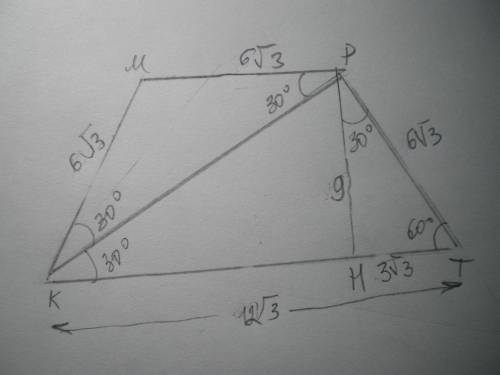
Дано: КМРТ - трапеция, КМ=РТ, ∠Т=60°, КР⊥РТ; КТ=12√3. Найти S(КМРТ).
Рассмотрим ΔКРТ - прямоугольный; ∠РКТ=90-60=30°, значит, РТ=0,5КТ=6√3 по свойству катета, лежащего против угла 30 градусов.
Проведем высоту РН и рассмотрим ΔРТН - прямоугольный;
∠ТРН=90-60=30°, значит, ТН=0,5РТ=3√3.
Найдем РН по теореме Пифагора:
РН²=РТ²-ТН²=108-27=81; РН=9.
Найдем МР. ∠МРК=∠РКН=30° как внутренние накрест лежащие при МР║КТ и секущей КР; ∠МКР=60-30=30°, значит, ΔКМР - равнобедренный, МР=КМ=6√3.
S(КМРТ)=(МР+КТ)/2 * РН = (6√3+12√3)/2 * 9=(9√3)*9=81√3 ед²
Обозначим трапецию АВСD, AB=CD, АD=12√3, ∠BAD=60°. ∠ABD=90°. Треугольник АВD- прямоугольный, ⇒ ∠АDB=180°-90°-60°=30°. Сторона АВ противолежит углу 30° и равна половине AD. АВ=6√3. Опустим высоту ВН на большее основание. Треугольник АВН - прямоугольный, ∠АВН=180°-90°-60°=30°. Катет АН=АВ:2=3√3. ⇒ DH=AD-AH=12√3-3√3=9√3. Высота ВН=АВ•sin60°=6√3•(√3/2)=9. Высота равнобедренной трапеции, проведенная из тупого угла, дели основание на отрезки, больший из которых равен полусумме оснований, меньший - их полуразности⇒ DH=(AD+BC):2. Площадь трапеции равна произведению высоты на полусумму оснований. S(ABCD)=BH•DH=9•9√3=81√3 (ед. площади)
решение смотри на фотографии