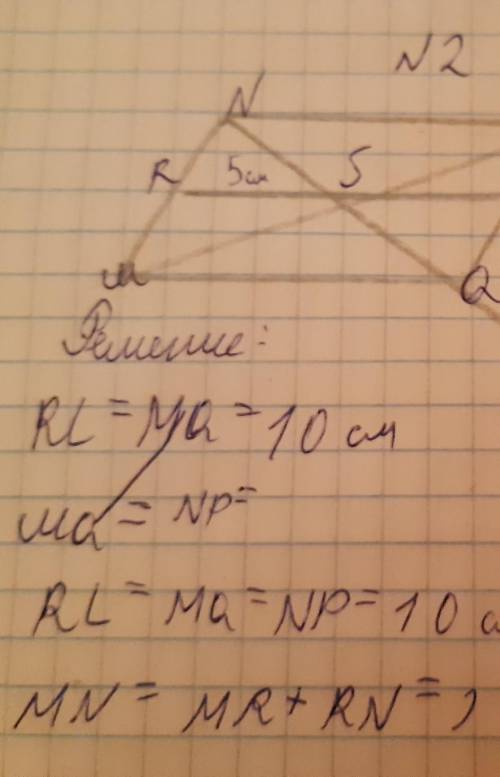
Пусть х градусов - первый угол, тогда 2х градусов - второй, (х+60) - третий угол, т.к. сумма углов треугольника равна 180 градусам то получим уравнение: х+2х+(х+60)=180 4х=120 х=30 => 30 градусов - первый угол, 60 градусов - второй угол, 90 градусов - третий угол.
Из вершины С параллельно диагонали ВD проведем прямую до пересечения с продолжением АD в точке Е.Углы САЕ и СЕА равны 60º(т.к. СЕ||ВD),АС=ВD и ВD=СЕ по построению, ⇒ треугольник АСЕ -равносторонний, АЕ=14см. ВС||АD, ВD||СЕ⇒ четырехугольник ВСЕD -параллелограмм, и DЕ=ВС. ⇒АЕ=АD+ВС=сумме оснований трапеции. Средняя линия трапеции равна полусумме оснований. Средняя линия равна 14:2 =7 см
Дан четырехугольник ABCD
AB=CD
BC=AD
угол A = 30⁰
E ∋ BC
угол CDE = 60⁰
Доказать. ABED - прямоугольная трапеция.
Доказательство.
Рассм. ABCD. угол A = 30⁰ ⇒ угол С = 30⁰
угол В = углу D = (360⁰ - 30⁰ - 30⁰)/2 = 300⁰/2 = 150⁰
угол ADE = угол ADC - угол CDE
т.к. угол ADC 150⁰, a по условию угол CDE = 60⁰, то угол AED = 150⁰ - 60⁰ = 90⁰
Опеределения:
- трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие не параллельны.
- трапеция, один из углов которой прямой, называется прямоугольной
Рассмотрим ABED - четырехугольник.
BE||AD,
AB не параллельно ED (т.к. ED перпендикуляр к AD)
угол EDA - 90⁰
След-но ABED - прямоугольная трапеция.
28 см
Объяснение:
R - середина MN по условию, значит если NR=2, то MN=2*2=4см.
Рассмотрим △MNQ. В нём RS - средняя линия, т.к. R - середина MN по условию, S - точка пересечения диагоналей, а точка пересечения диагоналей параллелограмма делит их пополам. Значит по свойству средней линии треугольника, RS ll MQ. Значит, продолжая отрезок RS до точки L пересечения с PQ мы получим параллелограмм MRLQ (по свойству, что в параллелограмме противоположные стороны попарно параллельны) => MQ=RL.
△MNQ=△PQN по свойству диагонали, значит и средние линии их равны, т.е. RS=SL. => MQ=2*RS=2*5=10 см
P=2*MN+2*MQ=2*4+2*10=28 см