Будем считать, что у отрезков есть начальная и конечная точки, то есть направление. Теперь у нас направленные отрезки (векторы).
Если точки расположены последовательно A_C, то имеем вектор AC.
Если точки расположены последовательно C_A, то имеем вектор -AC.
AM =1/2 AB =1/2 (AC+CB)
CK =1/2 CD =1/2 (CB+BD)
AK =AC+CK =AM+MK
AC +1/2 CB +1/2 BD = 1/2 AC +1/2 CB +MK => MK =1/2 AC +1/2 BD
1) Точки расположены последовательно A_C, B_D
MK =1/2 (AC+BD) = |5+7|/2 =6
2) Точки расположены последовательно C_A, B_D
MK =1/2 (-AC+BD) = |-5+7|/2 =1
3) Точки расположены последовательно A_C, D_B
MK =1/2 (AC-BD) = |5-7|/2 =1
4) Точки расположены последовательно C_A, D_B
MK =1/2 (-AC-BD) = |-5-7|/2 =6


Объяснение:
1
Диагонали ромба являются биссектрисами его углов:
<ВСD=2×<ACD=2×25=50 градусов.
Сумма соседних углов равна 180 градусов.
<АВС=180-<ВСD=180-50=130 градусов
2
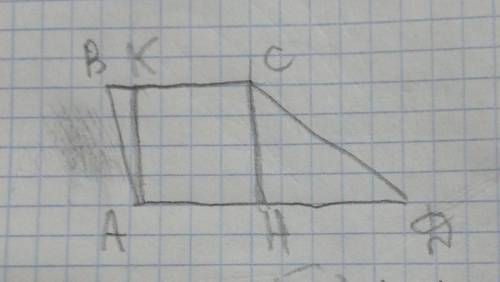
tg<A=BK/AK=8/12=2/3
3
SABCD=SHCD+SABCH
SHCD=1/2×HD×CH=1/2×5×4=10 cм^2
SABCH=(AH+BC)/2×CH=
=(4+5)/2×4=18 cм^2
SABCH=10+18=28 cм^2
Тр-к СНD:
По теореме Пифагора :
CD=корень (CH^2+HD^2)=
=корень (4^2+5^2)=корень (16+25)=
=корень41
Тр-к АВК:
АВ=корень (ВК^2+АК^2) =
=корень (1^2+4^2)=корень17
РАВСD=AB+BC+CD+AD=
=корень17+5+корень41+9=
=корень17+корень41+14
AB=24/sin60=16*sqrt(3), AB=BD, угол ABD=120гр. пО ТЕОРЕМЕ КОСИНУСОВ AD^2=AB^2+BD^2-2*AB*BD*cos120=2*AB^2+2*AB^2*cos60=6*256+3*256=9*256
AD=3*16=48
МОЖНО ЕЩЕ ПРОЩЕ.Из точки В опустить перпендикуляр на AD, пусть будет ВК и тогда треуг. ACB=треуг. ABK(по гипетенузе и острому углу) и получим AC=AK=24, тогда AD=48( высота в равнобедр.треуг. является медианой.)
Объяснение: