Решение:
В треугольнике АВС ВС=АВ,ВD---высота и биссектриса,если ΔАВС---равнобедренный,отсюда углы ВDС и BDA=90°.Следовательно смежные углы в сумме составляют 180 градусов,поэтому если ВС>AB (ВDС>90°),т.е. угол является тупым.
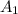 , вторую
, вторую 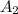 , третью
, третью 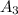 ,
,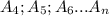 соответственно .
соответственно . 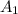 к остальным вершинам соответственно , тогда из неравенство треугольников получим неравенства
к остальным вершинам соответственно , тогда из неравенство треугольников получим неравенства 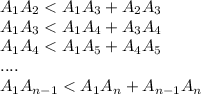
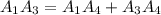 (это означает что треугольник не вырожденный) и подставляя получим требуемое то есть
(это означает что треугольник не вырожденный) и подставляя получим требуемое то есть 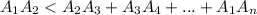
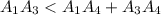
Рассмотрим треугольники АВD и СВD. Если ВС=АВ, то треугольник АВС равнобедренный и биссектриса является одновременно высотой, значит угол ВDС = углу BDA = 90 градусов. Эти смежные углы в сумме составляют 180 градусов, поэтому если ВС>AB, то угол ВDС>90 градусов, т.е. угол тупой.