МК=10 ед. изм.
Объяснение:
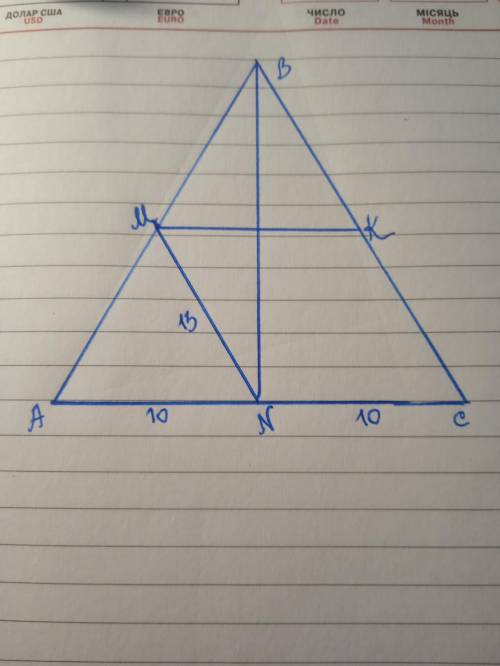
Дано: ΔАВС; АВ=ВС; МК, МN - средние линии; MN=13; BN=24. Найти МК.
ВС=2МN=26 по свойству средней линии треугольника
АВ=ВС=26;
ВN - медиана и высота, т.к. АN=СN по свойству средней линии треугольника
ΔАВN - прямоугольный;
по теореме Пифагора АN=√(АВ²-ВN²)=√(676-576)=√100=10.
АС=10*2=20.
МК=1/2 АС=10 ед. изм.
1.сумма углов четырехугольника равна 360,а так как один из углов прямой,то сумма остальних будет 360-90=270
составляем уравнение:
3х+8х+4х=270
15х=270
х=18
самый меньший у нас 18×3=54⁰
2.сумма углов равна 180×(n-2)
каждый угол равен
((180×(n-2))/n)=156
чтобы было понятней я напишу решение на бумаге
180n-360=156n
n=15
3.Полупериметр параллелограмма АВ+AD=16, BD=9 периметр треугольника ABD равен 16+9=25 см. ответ: 25 см
4.т.к сумма двух углов равна 100,то сумма других равна 360-100=260
260÷2=130⁰
5.)4×4.5=18(я тут не особо уверен)
6.)17×2=34
34-15=19
ответ:19
7.)ответ: 16.2
х-средняя линия
х+5.6-основание
х=(х+5.4)/2
2х=х+5.4
х=5.4 это средняя линия
2х=10.8 это основание
10.8-5.4=16.2
8.)10×2=20
36-20=16
16÷2=8
ответ:8
9.)большее основание равно:12
9=(х+х-6)/2
18=2х-6
24=2х
х=12
P.S на рисунке это 2 задание,тут решение может быть не понятным
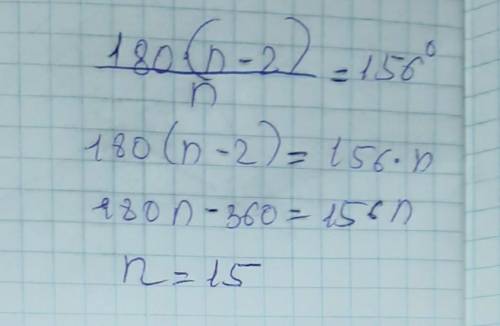
АВС, АВ = ВС, ВК - медиана к основанию АС и ВК = 24, МК - ср. линия (М - середина ВС) МК = 13. N - середина АВ.
Найти MN - ?
МК = АВ/2 = 13
Значит АВ = 26.
Из прям. тр-ка АВК по теор. Пифагора находим АК, которая и равна искомой MN:
ответ: 10 см.
Объяснение: