
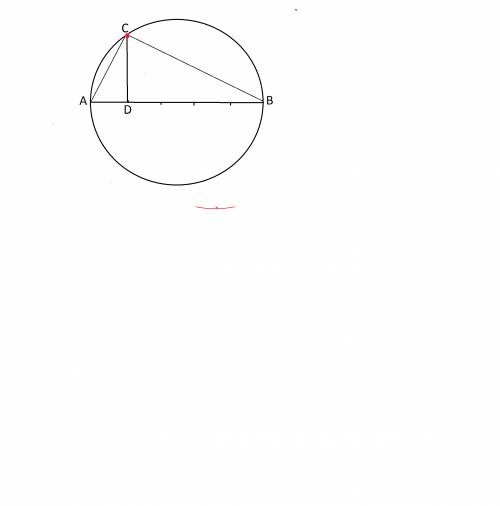
Сделаем рисунок.
АВ - диаметр, АС и СВ - катеты прямоугольного треугольника, поскольку вписанный угол АСВ опирается на диаметр и на дугу 180°, и потому равен 90°.
СD делит диаметр в отношении 1:4, следовательно, на 5 частей - отрезки 1/5 диаметра и 4/5
Диаметр окружности равен 2R =20см
АD=20:5=4 cм
DВ=20-4=16 см
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
DC- высота треугольника АСВ, т.к. по условию это перпендикуляр из С к диаметру, и является расстоянием от С до диаметра.
DC²=АD·DВ=4·16=64
DC=√64=8
СУММА векторов. Начало второго вектора совмещается с концом первого, сумма же есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом второго.
РАЗНОСТЬ. Для получения вектора разности (c) = (a-b) начала векторов соединяются и началом вектора разности (c) будет конец вектора (b) (вычитаемое), а концом — конец вектора (a) (уменьшаемое).
Исходя из этого:
1) |AB+BC|=|AC|, то есть |AB+BC|= а.
2) |AB+AC|=|AB+BC1|=|AC1|. АС1 - диагональ параллелограмма, построенного на векторах АВ и АС и вектор АС1 равен 2*АО. Вектор АО- высота равностороннего треугольника и равен а*√3/2. Значит АС1=а*√3.
|AB+AC|=а*√3.
3) |AB+CB|=|AB+C1B1|=|A1B1|. Вектор СВ переносим в конец вектора АВ, получаем вектор С1В1. Сумма - вектор АВ1. Вектор АВ1 по модулю равен вектору АС1.
|AB+CB|=а*√3.
4) |ВА-ВC|=|CA|=а.
5) |АВ-АC|=|CВ|=а.