Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы.
По т.Пифагора с²=a²+b², где с - гипотенуза, a и b – катеты.
с=√(9²+12²)=15
R=15:2=7,5 см
Подробно.
Центр описанной окружности треугольника лежит на пересечении срединных перпендикуляров к его сторонам.
Срединные перпендикуляры прямоугольного треугольника пересекаются на середине гипотенузы, следовательно центр описанной окружности - середина гипотенузы, и радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. R=7,5 см.
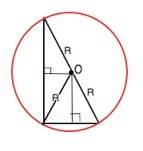
Назовем серединный перпендикуляр к стороне ВС-ОН. Треугольник НОВ=треугольнику НОС (по двум сторонам и углу между ними) ВН=НС (т. к. ОН-серединный перпендикуляр) , сторона ОН-общая, угол ОНВ=углу ОНС=90 (т. к ОН-перпендикуляр) . Тогда ВО=ОС=10. Расстоянием от точки О до АС-будет являться серединный перпендикуляр ОН1. Треугольник СН1 О-прямоугольный (СН1-перпендикуляр) , угол ОСН1=30 (это тот же угол АСО) . В прямоугольном треугольнике против угла в 30 градусов лежит катет равный половине гипотенузы, тогда ОН1=0,5 ОС=0,5*10=5
Объяснение:
Правильный ответ на вопрос «В треугольнике abc серединные перпендикуляры к сторонам AB и BC пересекаются в точке O, BO=10 см, угол ACO=30 градусов. Найдите расстояние ...» по предмету Геометрия
ответ
гіпотенуза = 25 м
Объяснение