Объяснение:
По второму признаку равенства треугольников: "Если сторона и два прилежащих к ней угла в одном треугольнике равны стороне и двум прилежащим к ней углам во втором треугольнике - то такие треугольники равны".
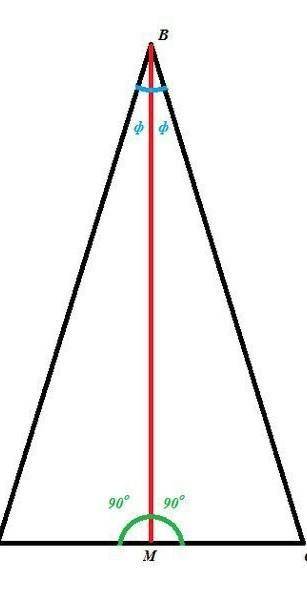
Нам дано, что BM - биссектриса (на рисунке) , значит угол ABM равен углу CBM по определению биссектрисы
Она же есть высота. По определению высоты BM перпендикулярна AC, значит углы AMB и CMB равны между собой (каждый по 90 градусов)
А также сторона BM - общая для треугольников ABM и CBM, значит эти два треугольника равны по 2-му признаку равенства треугольников.
В равных треугольниках против равных углов лежат равные стороны (и наоборот) . Прямые углы AMB и CMB равны, значит и стороны, лежащие против них AB и CB. По определению, треугольник, у которого две стороны равны, называется равнобедренным.
Утверждение доказано.
МОЖНО ЛУЧШИЙ ОТВЕТ!
Опустим перпендикуляр BB1 на плоскость a
Угол между наклонной и плоскостью - угол между наклонной и ее проекцией, ∠BAB1 =30
Опустим перпендикуляр BH на AC
BB1⊥a, BH⊥AC => B1H⊥AC (т о трех перпендикулярах)
Угол между плоскостями - угол между перпендикулярами к общей прямой, ∠BHB1 =45
BB1/AB =sin30
BB1/BH =sin45
cos(ABH) =BH/AB =sin30/sin45 =1/2 : 1/√2 =1/√2 => ∠ABH=45
BH - высота и биссектриса (△ABC - р/б), ∠ABC =2∠ABH =90
S(ABC) =1/2 AB*BC =4*4/2 =8 (см^2)