Здравствуйте!
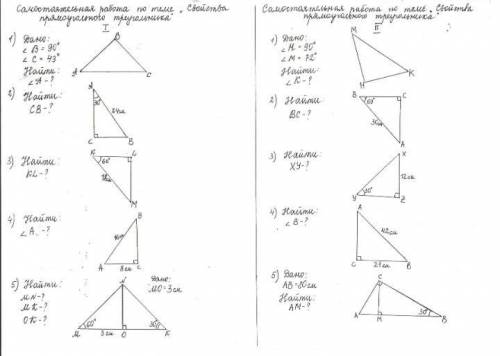
1).
∠1+∠2=180° смежные
∠1=2∠2 по условию
2∠2+∠2=180°
3∠2=180°
∠2=60°
∠1=2∠2=120°
2). Треугольники OBC и AOD равны по двум сторонам и углу между ними (AO=OB; CO=OD по условию; ∠СОВ=AOD -вертикальные) => ∠BCO=∠ABO как соответственные углы в равных треульниках.
AD || BC, т.к. накрест лежащие углы (∠BCO=∠ABO) равны. ЧТД.
3).
AB+AC+BC=34 см. (периметр)
AB=AC (боковые стороны)
BC (основание) =АВ+2 см= АС+ 2 см
BC+ (BC + 2 см)+(ВС+2 см) =34 см
3 ВС=30 см
ВС= 10 см
АВ=АС=10 см +2 см= 12 см
4). Треугольники АОВ и DOC равны по стороне и двум прилежащим углам (АО=ОD; ∠A=∠D по условию; ∠AOB=DOC вертикальные)
5). Проведем отрезок BD. Треугольники ABD и BDC- равнобедренные (AB=AD; BC=CD по условию) => ∠АВD=∠ADB и ∠CBD=∠CDB как углы при основании в р/б треугольнике.
∠В=∠АBD+∠CBD
∠D=∠ADB+∠CDB
А так как ∠АВD=∠ADB и ∠CBD=∠CDB, то ∠В=∠D.
6). Сумма острых углов прямогульного треугольника равна 90°.
∠A+∠B=90°
∠B=∠A-60° по условию
∠A+∠A-60°=90°
2∠A=150°
∠A=75°
∠B=∠A-60°=75°-60°=15°
7). Найдем ∠B. Сумма углов треугольника равна 180°.
∠А+∠В+∠С=180°
70°+55°+∠B=180°
∠B=180°-125°
∠B=55°
То есть ∠В=∠С=55°. А если углы в треуголнике равны, то треугольник равнобедренный. Основание BC.
7.1). Рассмотрим треугольник BMC. Он прямоугольный. Сумма острых углов прямоугольного треугольника равна 90°.
∠С+∠МBC=90°
55°+∠MBC=90°
∠MBC=35°
∠ABC=∠ABM+∠MBC
55°=∠ABM+35°
∠ABM=20°
1. 4 см.
2. 84 см.
3. 2√26 см.
Объяснение:
1. По Пифагору: ВС = √(АВ²-АС²) = √(9²-6²) = 3√5 см.
По свойству высоты из прямого угла прямоугольного треугольника:
СН = АС·ВС/АВ = 6·3√5/9 = 2√5 см.
По Пифагору: АН = √(АС²-СН²) = √(36-20) = 4 см.
ответ: 4 см.
2. По Пифагору второй катет равен √(37²-35²) = √(2·72) = 12см. Тогда периметр треугольника (сумма его трех сторон) равен:
37+35+12 = 84см.
ответ: 84см.
3. В ромбе стороны равны, а диагонали взаимно перпендикулярны и точкой пересечения делятся пополам.
Тогда в прямоугольном треугольнике АВО:
катеты АО=10см, ВО = 2см =>
гипотенуза АВ = √(10²-2²) = 2√26 см.
ответ: 2√26 см.
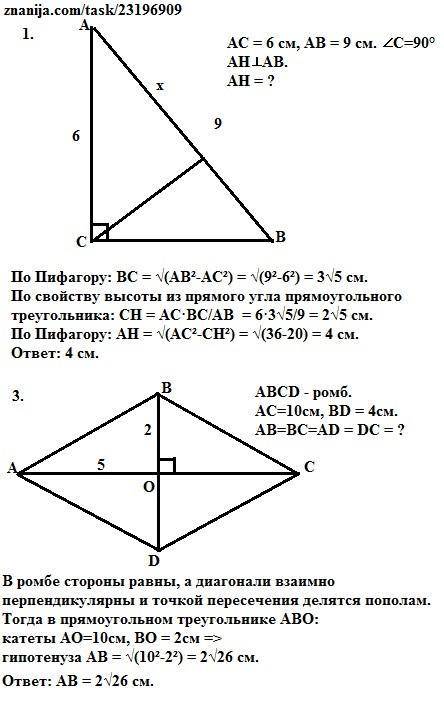
1. Решение: 90-72=18
В прямоугольном треугольнике угол можно найти: вычесть из 90 известный угол
ответ:18
2. AB в данном случае гипотенуза.
Угол А равен 30 градусов(90-60)
Свойство прямоугольного треугольника: катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы.
Следовательно: BC в 2 раза меньше AB.
BC=AB÷2.
BC=30÷2=15
ответ:15
3. XY в данном случае гипотенуза( так как лежит напротив прямого угла).
XZ - катет, лежащий напротив угла в 30 градусов. По задаче помним свойство прямоугольного треугольника: катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы.
Следовательно в обратную сторону: гипотенуза в два раза больше катета.
XY=2·XZ.
XY=2·12=24
ответ: 24
4. Видим, что AB - гипотенуза в 2 раза больше катета BC. Следовательно, уже известное нам свойство: катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы.
Значит угол, лежащий напротив BC равен 30 градусов. ∠A=30°
Оставшийся угол, который нам нужно найти по задаче(∠B) найдем также, как и в первой задаче: в прямоугольном треугольнике угол можно найти: вычесть из 90 известный угол. Значит ∠B=90°-30°=60°
ответ: 60
5. CM в большом прямоугольном треугольнике ΔABC - высота. Данная высота образует другой прямоугольный треугольник ΔAMC.
В ΔABC известен ∠B=30°. Следовательно, оставшийся ∠A=90°-30°=60°
Также нам известна гипотенуза AB=80. Следовательно, по свойству напротив ∠B=30° лежит катет, который равен половине гипотенузы. Катет AC=80÷2=40
Рассмотрим ΔAMC:
∠A мы нашли, он равен 60°
∠AMC=90°(так как CM- высота)
∠ACM=90°-60°=30°(свойство из первого задания)
В ΔAMC AC будет гипотенузой, а AM - катет, лежащий напротив угла 30°. Помним то же самое свойство: катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы.
Значит AM=AC÷2
AM=40÷2=20
ответ:20
Объяснение: