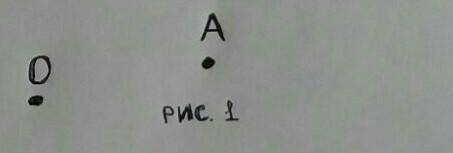
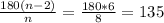градусов, значит, каждый угол восьмиугольника равен 135 градусов. Рассмотрим четырёхугольник АВСН, в нём два угла по 135 градусов и два по х градусов (АВ параллельна СН так как точки А и В равноудалены от точек С и Н, это получилась равнобедренная трапеция). В выпуклом четырёхугольнике сумма углов равна 360 градусов, таким образом 2х=90 градусов, следовательно, х=45 градусов. Отсюда мы можем найти углы DСН и GНС, которые равны по 135-х=90 градусов. Аналогично углы СDG и DGН равны по 90 градусов, значит, CDGH - прямоугольник. Одна сторона этого прямоугольника равна стороне восьмиугольника, теперь найдём вторую.
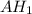и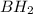 
. 
. 
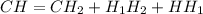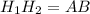, потому что получился прямоугольник, а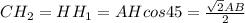 
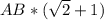
Вступление:
Пусть в прямоугольной трапеции ABCD, AB и CD основания, а ∠D прямой. Тогда AD меньшая боковая сторона (как расстояние между параллельными отрезками AB и CD), то есть AD=19см. По построению DC большое основание, поэтому по условию DC=31см. Острые углы при большом основании, ∠C=45° т.к. ∠D=90°.
H∈DC, BH⊥DC ⇒ BH=AD=19см.
В прямоугольном ΔBHC:
∠C=45°, ∠H=90° ⇒ ∠B=45°⇒ HC=BH=19см.
DH=DC-HC=31-19=12см.
В четырёхугольнике ABHD:
∠D=90°, ∠H=90° и ∠A=90°, ∠B=90° т.к. AB║DH, ведь H∈DC и AB║DC.
Получается ABHD - прямоугольник, поэтому AB=HD, HD=12см ⇒ AB=12см.
AB мень. осн. т.к. CD - большее.
Меньшее основание равно 12см.