ответ: два решения (одно для остроугольного треугольника, другое для тупоугольного...)
1) Р = 256 (см)
2) Р = 56V21 (см)
Объяснение: треугольник АВС, основание ВС=2а (чтобы не возиться с дробями); АВ=АС=b
P = 2a+2b = 2(a+b)
а=b*cos(B); по т.синусов: b=2R*sin(B)
S = 2a*h/2 = ah; h = b*sin(B)
S = P*r/2 = (a+b)*r
(a+b)*r = ab*sin(B)
b(1+cos(B))*r = b*b*sin(B)*cos(B)
(1+cos(B))*r = 2R*sin^2(B)*cos(B)
r/(2R) = (1-cos(B))*cos(B)
обозначим х=cos(B)
x^2 - x + (6/25) = 0
(5x)^2 - 5*(5x) + 6 = 0
по т.Виета корни (3) и (2)
5х=3 ---> х = 0.6
---> sin(B) = V(1-0.36) = 0.8 или
5х=2 ---> х = 0.4
---> sin(B) = V(1-0.16) = 0.2V21
b = 2*50*0.8 = 80 или
b = 2*50*0.2V21 = 20V21
a = 80*0.6 = 48 или
а = 20V21*0.4 = 8V21
P = 2*(80+48) = 128*2 = 256 или
Р = 2*(20+8)*V21 = 56V21
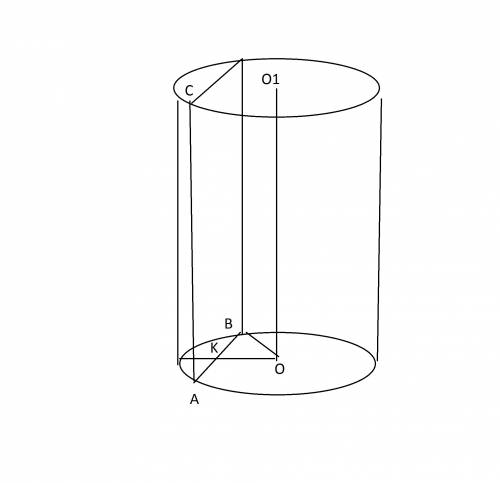
1)Дано: циліндр, АВСD- переріз, ВD-діагональ, R=АО=ОД=6 см, кут ВDА=60 градусів
Знайти: АВ, S abcd
з трикутника ВDА ( кут ВАD= 90 градусів)
tg60= AB/AD AD=AO+OD=12 см
AB=AD tg60
AB=12 * корінь з 3
Осьовим перерізом є прямокутник, отже
S=AB*AD
S=12коренів з 3 * 12=144 корінь з 3 (см2)
2)осьовим перерізом є прямокутник, а прямокутник, у якого діагоналі перпендикулярні - це квадрат, отже висота = 2R=10 см
3) з трикутника АВО ВО=R=5см, К-середина АВ, КО=4см,
з трикутника ВОК (кут ВКО = 90 градусів)
За т.Піфагора ВК= корінь квадратний 25-16= 3 см
АВ=2ВК=6 см
АС=h=8 cм
S= 8*6=48 (cм2)
4) АО=R=5см, KA і КВ - твірні, KA=13 cм , KO-?, Sakb-?
з трикутника КОА (кут КОА=90 градусів)
КО=корінь з 169-25=корінь з 144=12
S=АВ*КО/2 АВ=AO+OB=10
S=10*12/2=60 (см2)
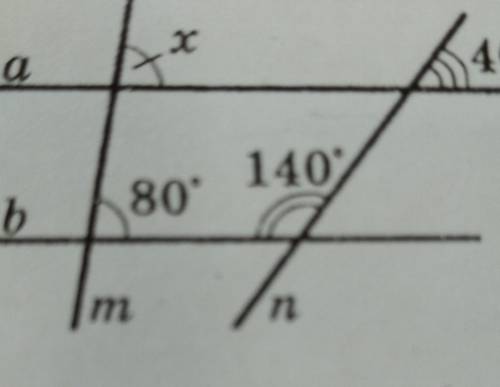
1. <1=<2 -по св-ву вертикальных кутов
Отже <1= 80
2. <1=<x по св-ву внешника накрест лежащих углов
Отже x=80