18 см
Объяснение:
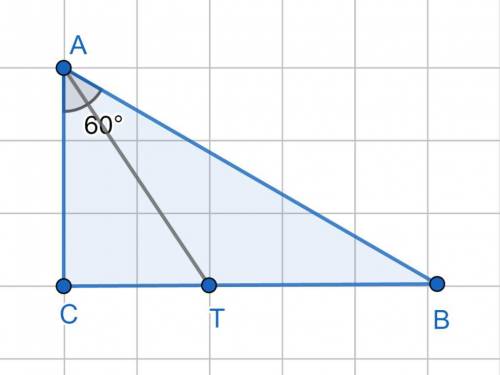
1) Т.к. <C = 90°, <BAC = 60°, то <ABC = 90° - 60° = 30°
2) AT - биссектриса, следовательно по определению она делит угол BAC пополам, а значит <CAT = <BAT = 60° : 2 = 30°.
3)Получаем, что в треугольнике ATB два угла равны 30°, следовательно этот треугольник равнобедренный, т.е. AT = TB = 12 см.
4) Рассмотрим ΔACT: он прямоугольный, <CAT = 30°. Катет лежащий напротив угла 30° равен половине гипотенузы, т.е. CT = AT : 2 = 12 : 2 = 6 (см)
5) CB = CT + TB = 6 + 12 = 18 (см)
8см,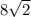 
см
Объяснение:
Наш треугольник прямоугольный и один из углов 45°, значит третий угол треугольника равен 90° - 45° = 45°.
Получается, что в треугольнике 2 равных угла по 45°, следовательно данный треугольник равнобедренный, следовательно катеты 
и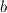 
равны, то есть второй катет тоже 8 см.
Гипотенузу 
находим по теореме Пифагора:
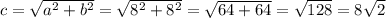(см)
P.S
Признак равнобедренного треугольника: если два угла треугольника равны, то такой треугольник равнобедренный
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов
180-100=80
80:2=40
AOB=40
Объяснение: