Параллелограмм.
CD = 12 см
AD = 3√3 см
∠ADC = 60˚
Найти:S - ?
Решение:Проведём высоту АЕ.
△DAE - прямоугольный, так как АЕ - высота.
"Сумма острых углов прямоугольного треугольника равна 90°".
=> ∠DAE = 90˚ - 60˚ = 30˚
"Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы".
=> DE = 3√3/2 см.
"Если угол прямоугольного треугольника равен 60°, то напротив лежащий катет равен произведению меньшего катета на √3".
=> AE = 3√3/2 * √3 = 9/2 = 4,5 см
S = CD * AE = 12 * 4,5 = 54 см²
ответ: 54 см²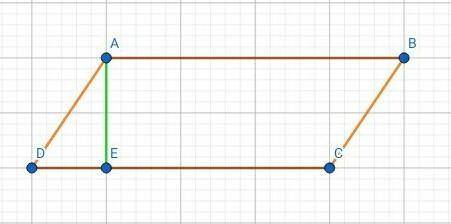
Ромб.
AC = 16 см.
BD = 30 см.
Найти:AB - ?
Решение:"Ромб - параллелограмм, у которого все стороны равны".
=> АВ = ВС = СD = AD.
Так как ромб - параллелограмм, вспомним свойства параллелограмма:
"У параллелограмма диагонали точкой пересечения делятся пополам".
=> АЕ = ЕС = 16/2 = 8 см, DE = EB = 30/2 = 15 см.
Теперь, вспомним свойства ромба:
"Диагонали ромба взаимно перпендикулярны и делят его углы пополам".
=> △АЕВ, △АЕD, △CED, △CEB - прямоугольные.
Найдём стороны АВ, ВС, CD, AD, по теореме Пифагора: (с = √(a² + b²), где с - гипотенуза; а, b - катеты)
√(8² + 15²) = √(64 + 225) = √289 = 17 см.
Итак, АВ = ВС = CD = AD = 17 см.
ответ: 17 см.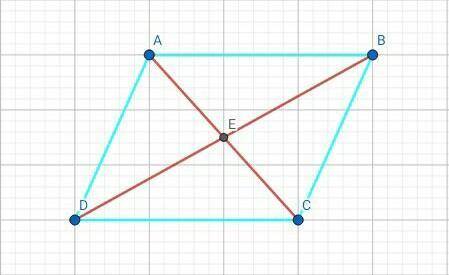
Эту задачу можно решить двумя .
1) Геометрический.
Так как плоскость отсекает на осях равные отрезки, то углы между осями и плоскостью равны.
Для примера возьмём угол к оси Oz.
Угол между прямой и плоскостью равен плоскому углу между этой прямой и её проекцией на плоскость.
Проекция оси Oz на плоскость лежит на прямой АД.
ОД = 4*cos 45 = 4*(√2/2) = 2√2.
Угол α = arc tg (2√2/4) = arc tg(√2/2) = 35,264 градуса.
2) Векторный.
Уравнение плоскости "в отрезках" (x/4) + (y/4) + (z/4) = 1.
В общем виде x + y + z - 4 = 0.
Направляющий вектор плоскости N = (1; 1; 1), его модуль равен √3.
Косинус угла между направляющим вектором плоскости и осью Oz равен: cos β = 1/√3. Сам угол равен arc cos(1/√3) = 54,7356 градуса.
Угол между нормалью к плоскости (прямой ее содержащей) и осями в сумме с искомым углом дают 90 градусов.
Тогда α = 90 - β = 90 - 54,7356 = 35,2644 градуса.