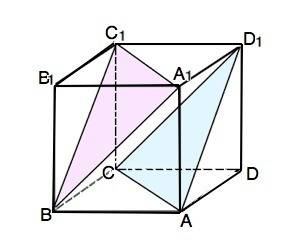
Докажите, что плоскость, проведённая через вершины А, D1 и С куба ABCDA1B1C1D1 параллельна плоскости, проведенной через вершины A1, B и C1
* * *
Диагонали противоположных граней куба, принадлеажщие одной плоскости, параллельны.
АС и А1С1 принадлежат плоскости диагонального сечения куба, А1В||D1C. Параллельны и ВС1 и АD1, принадлежащие плоскости ВС1D1А.
Если две пересекающиеся прямые (АС и АD1) одной плоскости параллельны двум пересекающимся прямым (A1C1 иBC1) (другой плоскости, эти плоскости параллельны.
1) АС=a√2=√2
2) ΔSKC, ∠К=90°,
∧ ∧
3) AB SC = DC SC= ∠SCK
cos∠SCK = CK/SC = 1/2 : 1 =1/2
4) Если cos∠SKC=1/2 , то ∠SKC=60°
5) Рассмотрим ΔBSD
SB=1 , SD=1 , BD=AC=√2
по т.косинусов BD²=SB²+SD²-2SB*SDcosS
(√2)²=1²+1²-2*1*1*cosS
2=2-2*cosS
2*cos∠S=2-2
2*cos∠S=0 ⇒ cos∠S=0, т.е ∠S=90°
∧
∠BSD= BS SD = 90°