Найдите углы равнобедренного треугольника, если один из его углов в пять раз меньше суммы двух других.
============================================================
Пусть ∠А = ∠С = х , ∠В = у, тогдаРассмотрим 2 случая решения данной задачи:Первый случай:∠В = ( ∠А + ∠С )/5у = 2х/5Сумма всех углов в треугольнике составляет 180° ⇒∠А + ∠В + ∠С = 180°х + 2х/5 + х = 18х°12х/5 = 180°х = 75°Значит, ∠А = ∠С = 75° , ∠В = 30°Второй случай:∠А = ( ∠В + ∠С )/5х = ( у + х )/55х = у + ху = 4хСумма всех углов в треугольнике составляет 180° ⇒∠А + ∠В + ∠С = 180х + 4х + х = 180°6х = 180°х = 30°Значит, ∠А = ∠С = 30° , ∠В = 120°ОТВЕТ: 30°, 75°, 75° ИЛИ 30°, 30°, 120°

Из большого угла проводим высоту к основанию, получаем прямоугольник и прямойгольный треугольник, находим углы в треуголнике.. основания в трапеции параллельны, поэтому проведенная высота дает прямой угол и к нижнему и к верхнему основания, тогда смотрим на больший угол равный 135, вычитаем из него прямой, получаем 45град, отсюда понимаем, что полученный треуольник прямоугольный равнобедренный, у нас известна гипотенуза, а квадрат гипотенузы, равен сумме квадратов катетов - находим катеты:
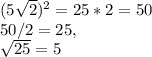
(находим квадрат гипотенузы, делим его на 2, и извлекаем корень квадратный, получаем катет)
Катет является и высотой, значит высота равна 5см, а длина прямоугольника равна 12-5=7см
Находим площадь трапеции:
-площадь прямоугольника=7*5=35
-площадь треульника=(5*5)/2=12.5
площадь трапеции=35+12.5=47,5см
9
Объяснение:
15²=АВ²-12²
225=АВ²-144
АВ²=81
АВ=9 см