Доказать подобие треугольников А1СВ1 и АВС.
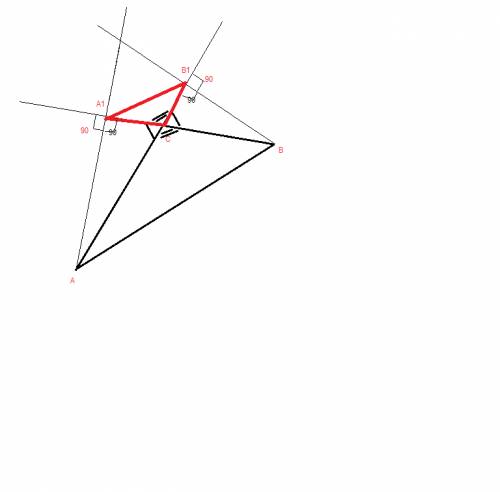
сделаем построение по условию
треугольники ACA1 и ВСВ1 - подобные по ПЕРВОМУ признаку подобия (по двум углам)
<AA1C=<BB1C=90 град
<ACA1=<BCB1 -вертикальные
следовательно , соответственные стороны относятся
СA1 / CB1 =CA / CB = k1 -коэффициент подобия для треугольников ACA1 и ВСВ1
отношение можно записать по-другому
СA1 / CA = CB1 / CB = k2 -коэффициент подобия для треугольников А1СВ1 и АВС.
т.е. треугольники А1СВ1 и АВС подобны по ВТОРОМУ признаку подобия
(если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны)
пропорциональные стороны СA1 / CA = CB1 / CB
<A1CB1 = <ACB --вертикальные
доказано подобие треугольников А1СВ1 и АВС.
Объяснение:
Треугольник FAC и его ортоцентр - это центр вписанной окружности треугольника ABC
Объяснение: Автор задания не совсем удачно обозначил центры вписанной и описанной окружностей. Обычно центр вписанной окружности - это точка I, центр описанной - точка O.
С разрешения автора буду считать, что центр вписанной окружности - это I. Кстати, картинка не совсем удачная. Дело в том, что, как известно, на одной прямой (прямой Эйлера) находятся центр O описанной окружности, центроид (то есть точка G пересечения медиан) и ортоцентр H. Центр же вписанной окружности лежит на этой прямой только если треугольник равнобедренный. Перехожу к решению.
Каждый из углов тр-ка ABC будем обозначать одной буквой - A, B, C. Значок градуса будем опускать. Из равнобедренного тр-ка EAC имеем: угол ECA=90-(A/2); из равноб. тр-ка ACD имеем: CAD=90-(C/2). Поэтому AFC=(A+C)/2. I лежит на биссектрисе угла BAC, то есть IAC=A/2, откуда DAI=DAC-IAC=90-(A+C)/2. То есть AFC+FAI=90, откуда AI перпендикулярно FC. Аналогично CI перпендикулярно AF. Следовательно, центр вписанной окружности треугольника ABC является по совместительству - ортоцентром треугольника FAC.