ответ: Р=162 см
Объяснение:
Пусть дана прямоугольная трапеция ABCD. у которой ВС и AD - основания, угол А =углу В=90 градусов. О- центр вписанной в трапецию окружности, точка М - точка касания окружности стороны AD и точка К - точка касания окружности стороны ВС. АМ=20 см, MD=25 см, тогда ОМ=ОК=r=20см и АВ=40 см. DM=DK=25 см как отрезки касательных,проведенных из одной точки. Угол С+ угол D трапеции=180 градусов, как внутренние накрест лежащие углы, DO и CO - биссектрисы соответствующих углов, то угол CDO+DCO=90градусов, следовательно угол COD=90 градусов, т.е. треугольник COD - прямоугольный, у которого ОК - высота, проведенная к гипотенузе, OK^2=DK*CK, CK=400/25=16 см. Значит периметр трапеции равен 20+25+25+16+16+20+40=162 см
V = 720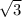 ≈ 1247,0766
≈ 1247,0766
Объяснение:
Треугольник ABD - прямоугольный.
Т.к. один его угол равен 30°, то второй угол = 180 - 90 = 60, т.е. это прямоугольный треугольник 30 60 90, а по его свойству, катет, противолежащий углу 30° (AD) равен половине гипотенузы (BD), т.е. гипотенуза BD равна:
BD = 2*AD = 2*12 = 24,
а катет, прилежащий углу 30° (AB) равен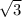 от противолежащего углу катета (AD), что доказывается теоремой Пифагора:
от противолежащего углу катета (AD), что доказывается теоремой Пифагора:
Итак:
AB = 12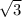 ;
;
Объем параллелепипеда равен произведению его сторон:
V = AA1 * AD * AB = 5 * 12 * 12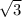 = 720
= 720