
Объяснение:
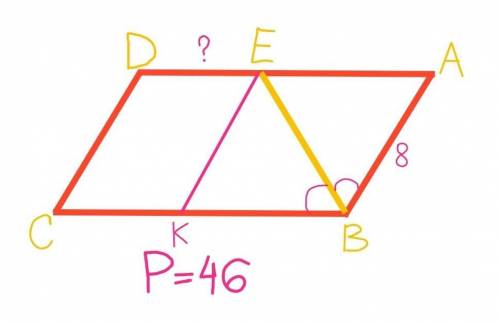
Из точки Е проведем отрезок ЕК, параллельный АВ.
Противоположные стороны параллелограмма параллельны, тоесть СВ//DE => ЕА//КВ и DE//CK
Так как в четырехугольнике КЕАВ стороны попарно параллельны, следовательно КЕАВ – параллелограмм.
ВЕ – биссектриса угла КВА по условию и диагональ параллелограмма КЕАВ.
Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм – ромб.
Следовательно: КЕАВ – ромб
У ромба все стороны равны. Исходя из этого: ЕА=КВ=АВ=8 см.
СD=AB=8 так как противоположные стороны параллелограмма равны.
Р(АВСD)=АВ+ВС+CD+AD=AB+BK+KC+CD+DE+EA=8+8+KC+8+DE+8=32+KC+DE
Так как Р(ABCD)=46 см по условию, то получим уравнение:
32+КС+DE=46
KC+DE=14 см
Так как ЕК//АВ, а АВ//CD, то ЕК//CD;
DE//CK (доказано ранее);
Исходя из этого: CDEK – параллелограмм.
Противоположные стороны параллелограмма равны, тоесть DE=CK.
Тогда 2DE=14 см
DE=7 см
ответ: 7 см
См. Объяснение
Объяснение:
Доказательство.
1) Так как, согласно условию задачи, АС = СD, то это означает, что треугольник ACD является равнобедренным, а сторона AD является основанием равнобедренного треугольника.
2) Так как точка М является серединой противоположной стороны АD, то это означает, что СМ является медианой, так как, согласно определению: медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, противоположной этой вершине.
3) Медианы равнобедренного треугольника обладают следующими свойствами: в равнобедренном треугольнике две медианы, проведенные к равным боковым сторонам треугольника, равны, а третья медиана, проведённая к основанию, одновременно является высотой, а также биссектрисой угла, из которого она проведена.
Это означает, что медиана СМ одновременно является высотой.
4) Согласно определению высоты: высота – это линия, проведённая из вершины треугольника перпендикулярно противоположной стороне.
Следовательно, высота СМ перпендикулярна AD, - что и требовалось доказать.