Вариант решения.
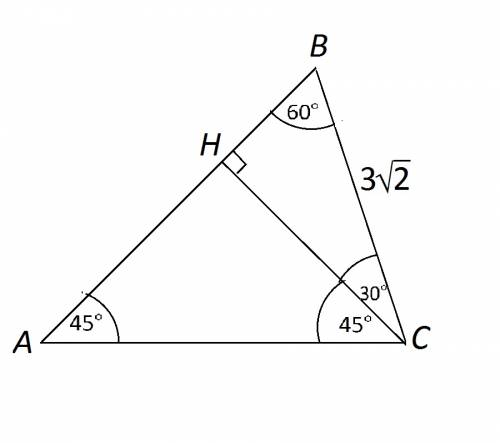
Проведём из С к АВ высоту СН
Она разделила угол С на углы 45° и 30°
Получены треугольник ВНС с углами 30° и 60°и равнобедренный АНС с 45° при основании АС.
СН из треугольника ВНС равен ВС*sin (60°)=(3√2)*(√3):2.
Умножив числитель и знаменатель в значении СН на √2, получим (3√3):√2
Гипотенуза равнобедренного прямоугольного треугольника равна а√2
АС=АВ*√2={(3√3):√2}*√2=3√3
--------
Или:
СН, как противолежащий углу 30° катет, равен половине ВС и равен 1,5√2
Тогда по т. Пифагора СН²=ВС²-ВН²=18-4,5=13,5
АН=СН
АС²=АН²+СН²=13,5+13,5=27
АС=√27=√9*√3=3√3
Как видим, любой вариант дает одинаковый ответ.
Дано:треуг АВС-равн, АС=6см., АВ=5см
Найти:ВМ=?
Решение:
Рассмотрим треуг. АВС
1)треуг АВСравноб. по усл.
2)АВ=ВС=6см, по определению равн. треуг.
3) т.к. ВМ высота, то она является и медианой - по свойству равноб. треуг. Значит АМ=МС=6:2=3см.
Рассмотрим треуг АВМ
1)треуг АВМ прямоуголь. т.к. ВМ высота, то <АМВ=<ВМС=90°
2) Найдём ВМ, через теорему Пифагора
5^2=3^2+ВМ^2
ВМ^2=25-9=16
ВМ=√16=4см
ответ: ВМ=4см.