Найти :Решение :В прямоугольном треугольнике высота, проведённая к гипотенузе - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.
Следовательно,
Площадь прямоугольного треугольника равна половине произведения его катетов.
Следовательно, ед².
ответ :
64 ед².
- - -
70. ABCD - прямоугольник. Найдите .
- - -Дано :
Четырёхугольник ABCD - прямоугольник.
АС - диагональ.
HD⊥АС.
HD = 6, АН = 9.
Найти :
Решение :Прямоугольник - это параллелограмм, все углы которого прямые.
Следовательно ∠D = 90°.
Рассмотрим ΔACD - прямоугольный.
В прямоугольном треугольнике высота, опущенная на гипотенузу - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.
Следовательно,
Площадь треугольника равна половине произведения высоты и стороны, на которую опущена эта высота.
Следовательно, ед².
Диагональ параллелограмма делит параллелограмм на два равновеликих (равных по площади) треугольника.
1)а. Возьмем тр. АВС с основанием АС.угол В=62 => угол А=угол С => 58= сторона АС большая.( против бОльшего угла лежит бОльшая сторона) б. Возьмем тр. АВС с основанием АС. угол В = 58 => угол А= угол С = 61=> стороны АВ и ВС большие ( в равнобедренном треугольнике 2 стороны равны) 2)а. рассмотрим тр. АВС, где угол А> угол В> угол С=> сторона ВС >сторона АС> сторона АВ б. рассмотрим тр. АВС, где угол А = угол В< угол С => сторона АС = сторона ВС< сторона АВ 3)нет. против большего угла лежит большая сторона, а тупой угол всегда является самым большим в треугольнике. 4) задачу можно решить, только если точка N находится вне треугольника АОВ. рассмотрим треугольники АОN = ВОN (АN=ВN, угол ОАN=угол ОВN, ОN- общая)=> угол АОN = угол ВОN => точка N лежит на биссектрисе угла АОВ.
68. По данным на рисунке найдите площадь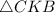 .
.
- - -Дано :ΔСКВ - прямоугольный (∠С = 90°).
СК - высота (СК⊥АВ).
АК = 4, КВ = 16.
Найти :Следовательно,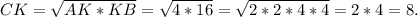
Площадь прямоугольного треугольника равна половине произведения его катетов.Следовательно,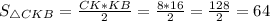 ед².
ед².
ответ :64 ед².
- - -70. ABCD - прямоугольник. Найдите .
.
- - -Дано :Четырёхугольник ABCD - прямоугольник.
АС - диагональ.
HD⊥АС.
HD = 6, АН = 9.
Найти :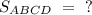
Решение :Прямоугольник - это параллелограмм, все углы которого прямые.Следовательно ∠D = 90°.
Рассмотрим ΔACD - прямоугольный.
В прямоугольном треугольнике высота, опущенная на гипотенузу - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.Следовательно,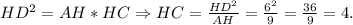
Площадь треугольника равна половине произведения высоты и стороны, на которую опущена эта высота.Следовательно,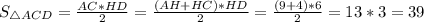 ед².
ед².
Диагональ параллелограмма делит параллелограмм на два равновеликих (равных по площади) треугольника.Тогда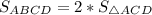 = 2*39 ед² = 78 ед².
= 2*39 ед² = 78 ед².
ответ :78 ед².