а) BC1 || AD1, поэтому угол между прямыми AB1 и BC1 равен углу между AB1 и AD1.
ребро куба равно а, поэтому (так как грани куба - квадраты), то AB1=AD1=B1D1, а значит треугольник AB1D1 - правильный(равносторонний),
углы равностороннего треугольника равны 60 градусов,
значит искомый угол между прямыми AB1 и BC1 равен 60 градусов
б) так как В1С1 - перпендикуляр с точки С1 на грань АА1В1В, то угол между прямой AC1 и гранью AA1B1B равен углу В1АС1
(треугольник АВ1С1 - прямоугольным с прямым углом АВ1С1)
по свойству диагонали квадрата 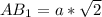
по свойству диагонали куба 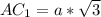
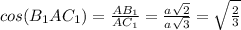
угол В1АС1 равен arccos корень(2/3)т.е.
угол между прямой AC1 и гранью AA1B1B равен arccos корень(2/3) градусов
В таких заданиях в основном ведётся работа с формулами. Прежде, чем притупить к заданям, вспомним формулу основного тригоносетрического тождества, которая в основном тут и будет использоваться:
1) Если мы воспользуемся основным тригоносетрическим тождеством, выразив оттуда косинус в квадрате, то получим как раз таки это выражение, значит его можно упростить так:
2) Аналогично предыдущему, тоже опираясь на основное тригоносетрическое тождество, получим:
3) Это выражение для начала можно сложить по формуле разности квадратов, после чего преобразуем полученное выражение так же, как и во втором:
4) Опять же, опираясь на основное тригоносетрическое тождество можно синус в квадрате плюс косинус в квадрате заменить на единицу, в результате чего мы получим:
5) Вынесем за скобку синус, а полученное выражение преубразуем, опять же, как во втором пункте: