Вступление:
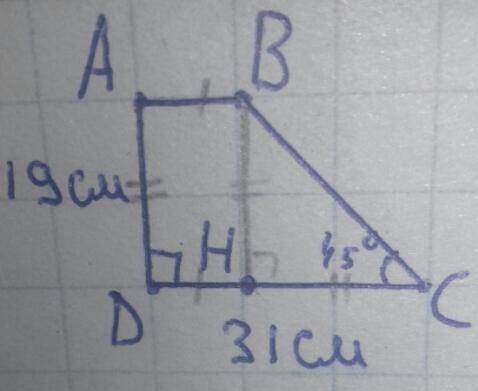
Пусть в прямоугольной трапеции ABCD, AB и CD основания, а ∠D прямой. Тогда AD меньшая боковая сторона (как расстояние между параллельными отрезками AB и CD), то есть AD=19см. По построению DC большое основание, поэтому по условию DC=31см. Острые углы при большом основании, ∠C=45° т.к. ∠D=90°.
H∈DC, BH⊥DC ⇒ BH=AD=19см.
В прямоугольном ΔBHC:
∠C=45°, ∠H=90° ⇒ ∠B=45°⇒ HC=BH=19см.
DH=DC-HC=31-19=12см.
В четырёхугольнике ABHD:
∠D=90°, ∠H=90° и ∠A=90°, ∠B=90° т.к. AB║DH, ведь H∈DC и AB║DC.
Получается ABHD - прямоугольник, поэтому AB=HD, HD=12см ⇒ AB=12см.
AB мень. осн. т.к. CD - большее.
Меньшее основание равно 12см.
С чертежом нельзя :
Поскольку DC паралелльно АВ и лежит не в плоскости альфа, то она (DC) паралелльна плоскости альфа. Поэтому расстояние от плоскости альфа до любой точки этой прямой - величина постоянная. В том числе и расстояние от точек C и D, и по условию это a/2.
Двугранный угол рисовать я не буду, в плоскости ромба надо провести перпендикуляр из точки D на АС (пусть это будет DE), длинна этого перпендикуляра DE = a*sqrt(3)/2 (то есть сторона AD, умноженная на синус 60 градусов). Кроме того, если опустить перпендикуляр на плоскость альфа из точки D (пусть это будет DF), и провести плоскость через три точки D, E, F, то эта плоскость перпендикулярна прямой АВ (АБ перпендикулярна 2 прямым этой плоскости - DE и DF), и FED - как раз и есть двугранный угол. Треугольник FED прямоугольный, гипотенуза DE, катет DF = a/2. То есть, если DE умножить на синус двугранного угла, то получится a/2.
Отсюда синус это равен sqrt(3)/3.