
0,25
Объяснение:
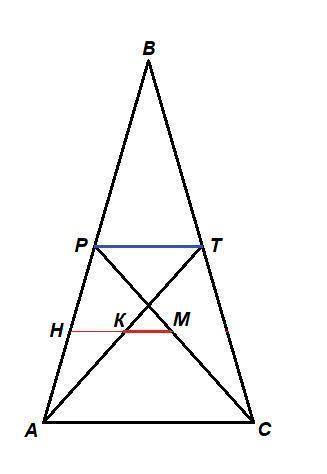
АТ и СР - медианы, проведенные к боковым сторонам равнобедренного треугольника АВС.
РТ - средняя линия треугольника АВС, значит
РТ = 1/2 АС = 1/2 · 1 = 0,5
Пусть М - середина СР. Проведем МН║АС (Н ∈ АВ), тогда по теореме Фалеса Н - середина АР.
МН - средняя линия треугольника АРС, значит
МН = 1/2 АС = 0,5
МН пересекает АТ в точке К.
Н - середина АР, НК║АС, а значит и НК║РТ, ⇒ по теореме Фалеса К - середина АТ.
НК - средняя линия треугольника АРТ.
НК = 1/2 РТ = 1/2 · 0,5 = 0,25
КМ - искомый отрезок.
КМ = МН - НК = 0,5 - 0,25 = 0,25
S=πRl+πR², ( l образующая)
Sполн.пов.=πR*(l+R)
1. сечение конуса - равнобедренный прямоугольный треугольник: гипотенуза - хорда х=6, катеты - образующие конуса l.
по теореме Пифагора:
x²=l²+l², 6²=l²+l², l²=18, l=3√2
2. осевое сечение конуса - равнобедренный треугольник основание - диаметр основания конуса d, боковые стороны - образующие конуса l.
по теореме косинусов: d²=l²+l²-2*l*l*cos120°
d²=18+18-2*√18*√18*(-1/2)
d²=54, d=3√6. R=1,5√6
S=π*1,5(√6*3√2+1,5)=1,5*π*(6√2+1,5)
S=1,5π*(6√2+1,5)