Вправильной треугольной пирамиде сторона основания равна 12 см, а боковое ребро 10 см. найдите: 1) высоту пирамиды ; 2)угол, образованный боковым ребром и плоскостью основания пирамиды; 3)угол междубоковой гранью и плоскостью основания пирамиды; 4)площадь боковой поверхности пирамиды; 5)площадь полной поверхности пирамиды; 6)объем пирамиды; 7)площадь сечения, проходящего через высоту основания и высоту пирамиды; 8)площадь сечения, проходящего через середину высоты пирамиды, параллельнооснованию; 9)площадь сечения, проходящего через высоту основания и середину боковой стороны.
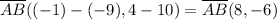 ;
; от точки A
от точки A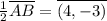 ;
; в обе возможные стороны
в обе возможные стороны перпендикулярен вектору основания
перпендикулярен вектору основания  , а значит его проекции накрест-пропорциональны с противоположным знаком:
, а значит его проекции накрест-пропорциональны с противоположным знаком: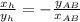 , что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:
, что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:  (II) ;
(II) ; пропорционален вектору
пропорционален вектору  , поскольку для вектора
, поскольку для вектора  выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора
выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора  ;
; имеет длину
имеет длину 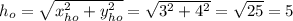 ;
;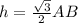 , т.к
, т.к 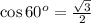 ;
;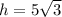 , а стало быть
, а стало быть  ;
;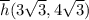 .
.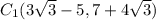 /// примечание:
/// примечание: 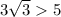 ;
;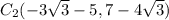 /// примечание:
/// примечание: 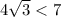 .
.
Основание пирамиды - правильный треугольник. Вершина пирамиды проецируется в центр О треугольника. Высота правильного треугольника АН по формуле: h=а*√3/2, где а - сторона треугольника. AH=12√3/2 = 6√3см. В правильном треугольнике высота=медиана=биссектриса. По свойству медианы (центром правильного треугольника делится в отношении 2:1, считая от вершины). АО=(2/3)*h = 4√3см. OH=2√3см.
1. По Пифагору: SO=√(AS²-AO²) = √(100-48) = 2√13см.
2. Cos(SAO) = AO/AS =4√3/10 = 0,4√3 ≈ 0,693.
<SAO = arccos(0,693) ≈46,1°.
3. Апофема по Пифагору: SH=√(SO²+OH²)=√(52+12) = 8см.
Sin(SHO) = SO/SH =2√13/8 ≈ 0,9. <SHO = arcsin(0,9)≈ 64,2°.
4. Все три грани пирамиды равны. Sбок = (1/2)*а*SH*3 = 144см².
5. Sполн = Sбок+So =144+(1/2)*a*h= 144+(1/2)*12*6√3=144+36√3см².
6. Объем пирамиды V = (1/3)So*SO = (1/3)36√3*2√13 = 24√39 см³.
7. Sc = (1/2)*AH*SO = (1/2)*6√3*2√13 = 6√39 см².
8. Sсеч = So/4 = 36√3/4 = 9√3см². (так как площади подобных треугольников относятся как квадрат коэффициента подобия, а k=2, поскольку параллельное сечение делит высоту пирамиды пополам).
9. Сечение - треугольник АМН с стороной АН=6√3см, и сторонами AM и НМ. Найдем эти стороны.
В правильной пирамиде углы α наклона боковых ребер к сторонам основания равны. Cosα = HC/SC = 6/10=0,6. В треугольнике АМС по теореме косинусов АМ=√(АС²+МС²-2АС*МС*Cosα) = √(169-72) = √97. В треугольнике HМС HМ=5, как средняя линия треугольника CBS. По теореме косинусов в треугольнике АМН:
Cos(<AMH) = (AM²+MH²-AH²)/(2*AM*MH) = (97+25-108)/(10√97) ≈ 0,142. Sin(<AMH) = √(1- 0,142²) = √0,9798 = 0,9898.
Тогда площадь сечения АМН= (1/2)АМ*МН*Sin(<AMH) или
Samh = √97*5*0,9898/2 ≈24,4см².