1) Через две различнье точки всегда можно провести окружность.
ДА
2) Через две различные точки всегда можно провести окружность , и притом только одну.
НЕТ, окружностей бесконечно много.
3) Через две различные точки всегда можно провести окружность данного радиуса.
НЕТ, если расстояние меж точками больше диаметра окружности - то её не построить
4) Через две различные точки всегда можно провести окружность радиуса, paвного между этими точками , и притом только одну.
Ошибка в вопросе!
Если расстояние меж точками = диаметру окружности - то да, её можно построить только одну.
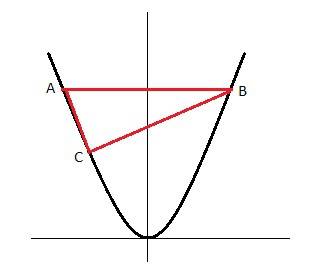
Треугольник АВС. АВ И ВС - катеты, угол С=90 градусов. Так как треугольник - прямоугольный, то его площадь - это половина произведения катетов. S=0.5*а*b
В любом треугольнике площадь высчитывается по формуле "половина основания умножить на высоту*. Высота, проведенная из прямого угла к гипотенузе, равна h по условию, гипотенуза=c по условию. Тогда S=0.5*c*h
Так как это один и тот же треугольник, то 0.5*а*b=0.5*c*h
делим правую и левую части на 0.5 и получаем искомое равенство. a*b=c*h. Что и требовалось доказать.