Объяснение:
Часть прямой линии, расположенная по одну сторону от любой точки, лежащей на этой прямой, называется лучом. Можно луч называть полупрямой.
Если лучи лежат на одной прямой, имеют общее начало и расположены по одну сторону от начальной точки, они совпадают.
Луч с началом в точке A можно обозначить и как AB, и как AC.
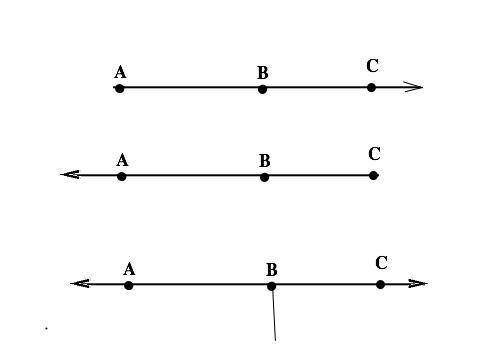
Лучи АВ и АС - совпадают ( имеют общее начало А и расположены по одну сторону от него).
Лучи СВ и СА – совпадают ( имеют общее начало С и направлены в одну сторону. )
ВА и ВС - противоположные (их еще называют дополнительными). Они лежат на одной прямой, имеют общее начало В, но направлены в противоположные стороны. Они дополняют друг друга до прямой.
Проведем радиусы OA и OB. Они будут равными как радиусы одной окружности. Проведем высоту OH, которая будет являться одновременно радиусом вписанной окружности и равна 3 по условию. Так как треугольник равнобедренный, то OH будет также являться медианой. Так как, AB - сторона многоугольника и основание треугольника AOB, равная 6√3, а OH - медиана, то AH = (6√3)÷2 = 3√3. Так как треугольник AOH - прямоугольник, а OA - гипотенуза, то воспользуемся т. Пифагора: OA = √((3√3)²+3²) = √36 = 6. Значит, радиус OA описанной окружности равен 6.