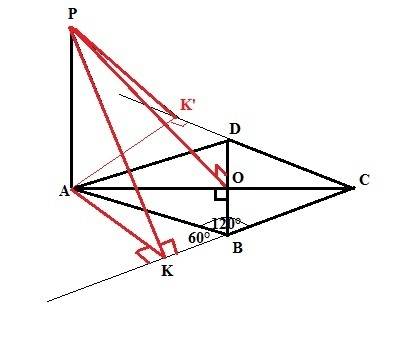
В ромбе диагонали взаимно перпендикулярны, точкой пересечения делятся пополам и являются биссектрисами углов. Проведем перпендикуляр из точки Р к прямой СВ. Так как угол АВС=120°, этот перпендикуляр пересечет прямую СВ в точке К на продолжении стороны СВ ромба. В прямоугольном треугольнике АКВ угол АВК=60°, как смежный угол с углом АВС=120°. Следовательно, катет АК равен а*Sin60 или АК = а√3/2. В прямоугольном треугольнике РАК (сторона РК перпендикулярна прямой КС по теореме о трех перпендикулярах) гипотенуза РК по Пифагору равна РК=√(а²+3а²/4) = а√7/2. Это и есть искомое расстояние от точки Р до прямой ВС. Заметим что расстояние от точки Р до прямой CD равно расстоянию от точки Р до прямой ВС в силу симметричности ромба относительно диагонали АС. Расстояние от точки Р до прямой BD - это отрезок РО (перпендикулярный прямой BD по теореме о трех перпендикулярах), где точка О - точка пересечения диагоналей. Поскольку треугольники АКВ и АОВ равны по гипотенузе АВ и острому углу, АО=АК =>
РО = РК = а√7/2.
ответ: расстояние от точки Р до прямых АВ, CD и BD одинаково и равно а√7/2 ед.
треугольник АВС
АВ=ВС
угол АВД=уголДВС
АД=ДС
Д-ть, что АКС равнобедренный
Доказательство
Рассмотрим треугольники АКВ и СКВ ВК - общая АВ= ВС как стороны равнобедренного треугольника. Угол АВД= угол ДВС так как в равнобедренном треугольнике медиана является биссектрисой и высотой. Если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника то такие треугольники равны. Если треугольники равны то и соответствующие стороны равны АК=КС боковые стороны треугольника АКС.АД=ДС КД перпендикулярно АС Следовательно треугольник равнобедренный