Площадь равнобедренного треугольника равняется произведению высоты на половину длины основания, то есть
S=ВД*АС/2=5*10√3/2=25√3 см²
ответ: высота ВД=5см, площадь S=25√3 см², углы треугольника равны 30°, 30°, 120°.
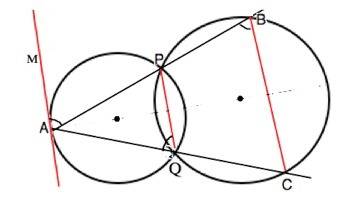
Через т.А проведем касательную АМ
АР- хорда, ∠МАР =дуга АР:2 ( свойство угла между касательной и хордой)
Вписанный ∠АQP=дуга АР:2 ( свойство вписанного угла)⇒
∠МАР=∠АQP.
∠РQC +∠PQA=180°
Во второй окружности сумма противоположных углов вписанного четырехугольника PBCQ равна 180° (свойство), ⇒
∠РQC+<PBC=180° Следовательно, ∠АВС=∠PQA.
Так как ∠PQA=∠PAM, то ∠ABC=∠BAM. Они накрестлежащие, а равенство накрестлежащих углов при пересечении двух прямых секущей – признак параллельных прямых.⇒
МА║ВС , что и требовалось доказать.
4√3см
Объяснение:
Диагонали ромба пересекаются перпендикулярно и точкой пересечения делятся пополам
ВО=ВD/2=3/2=1,5
Диагонали ромба являются биссектриссами углов.
<ВАС=<ВАD:2=120°:2=60°
sin<BAO=BO/AB
sin60°=√3/2
√3/2=1,5/AB
AB=1,5*2/√3=√3см
P(ABCD)=4*AB=4√3см