Объяснение:
По теореме Пифагора :
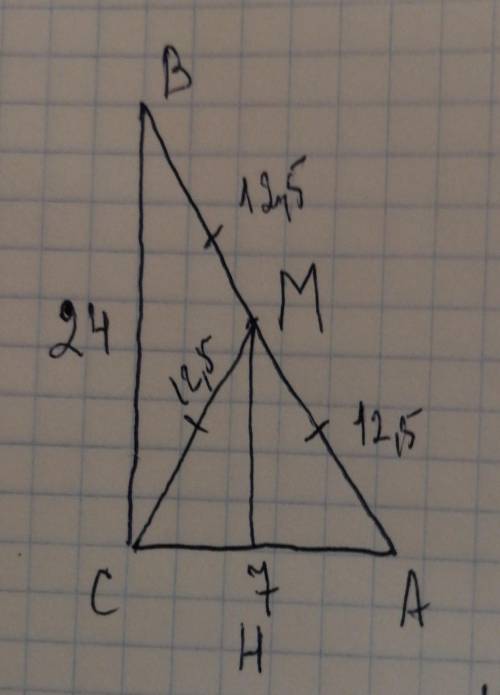
АВ=корень (ВС^2-АС^2)=
корень (24^2-7^2)=корень (576+49)=
=корень 625=25 см
Медиана, проведённая из вершины прямого угла равна половине гипотенузы :
СМ=1/2×АВ=1/2×25=25/2=12,5 см
Острый угол между гипотенузой и медианой
это угол СМА, т. к против меньшей стороны лежит меньший угол (у тр-ков ВСМ и СМА боковые стороны равны, а сторона АС меньше стороны ВС, значит <СМА меньший)
Тр-к СМА - равнобедренный (СМ=АМ),
МН - высота и медиана.
АН=АС:2=7:2=3,5 см
Тр-к НМА - прямоугольный,
По теореме Пифагора :
МН=корень (АМ^2-АН^2) =
=корень (12,5^2-3,5^2)=корень 144=12 см
S=1/2×AC×MH=1/2×7×12=42 cм^2
S=1/2×CM×AM×sin<CMA=
=1/2×12,5×12,5×sin<CMA
42=78,125×sin<CMA
sin<CMA=42:78,125=0,5376
По теореме косинусов :
cos<CMA=(CM^2+AM^2-AC^2)/(2×CM×AM) =
=(12,5^2+12,5^2-7^2)/(2×12,5×12,5)=
=(156,25+156,25-49)/312,5=
=263,5/312,5=0,8432
ответ : sin<CMA=0,5376
cos<CMA=0,5376
Пусть(Не пиши пусть) СН-Высота
Диагональ ВD пересекает СН в точке О, СО=20 см, ОН=12 см.
ВС=СD.
∆ ВСD - равнобедренный угол СВD=углу СDВ.
В то же время ∠СВО=∠НDО как накрестлежащие при пересечении параллельных прямых секущей, углы при О - равны как вертикальные. прямоугольные треугольники ВСО и НDО подобны.
HD:ВС=ОH:СО=12\20=3/5
Примем ВС=СD=а.
Тогда НD=3а\5
Из ∆ СНD по т.Пифагора
СD²=СН²+НD²
а²=1024+9а²\25
16а²\25=1024
Разделим обе стороны уравнения на 16, извлечем корни:
а\5=8
а=40 см
АD=а+3а\5=1,6а
АD=40х1,6=64 см
S=(BC+AD)хCH:2=104х(20+12):2=1664 см²
х-это умножение)