Боковые грани правильной пирамиды - равнобедренные треугольники с боковыми сторонами, равными боковому ребру и основанием, равным стороне основания пирамиды.
Площадь боковой поверхности - сумма площадей трех равных граней. Боковое ребро найдено =16.
Найти сторону АВ основания длина описанной окружности.
R=a:√3 - формула радиуса описанной окружности правильного треугольника, где а- сторона треугольника. ⇒
а=R•√3⇒
АВ=8•3=24
S ∆ AMB=MH•AB:2=MH•AH
Из ⊿ МОН по т.Пифагора
МН²=МО²+ОН²
ОН - радиус вписанной в правильный треугольник окружности и равен половине радиуса описанной,⇒
ОН=4√3
МН=√(МО²+ОН²)=√(64+48)=√112=4√7⇒
S бок=3•S∆ AMB=3•12•4√7=144√7 см²
Для вычисления поверхности, необходимо знать размер квадрата-основания призмы.
Диагональ призмы, ее вертикальное ребро и диагональ основания составляют прямоугольный треугольник с известными углом и длиной противолежащего катета (высота призмы).
Вторым катетом является диагональ основания, длиной (12·√2)·ctg30°=12·√2·√3=12·√6см.
Длина стороны квадрата-основания равна 12·√6·cos45°=12·√6·√2/2=6·√12см.
Площадь основания: (6·√12)²=36·12=432 см²
Площадь боковой грани: (12·√2)· (6·√12)=72√24 см²
Полная площадь поверхности: S=2·432+4·72√24=864+288√24≈864+1411=2275 см²
r = 4,5
Объяснение:
ВС = 48 - 15 - 15 = 18 см
AD - высота и медиана (т.к. треугольник равнобедренный)
Тогда ΔABD - прямоугольный. АВ = 15, BD = 9
По теореме Пифагора AD = √15² + 9² = √144 = 12
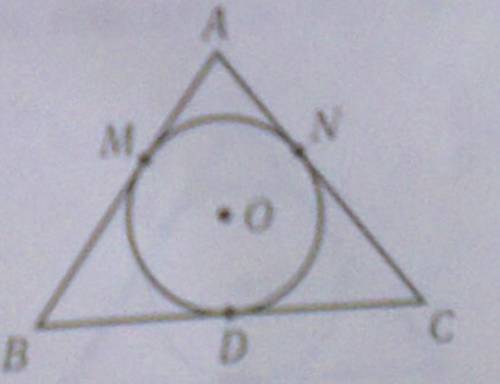
О - точка пересечения биссектрис
ΔODB = ΔOMB т.к.
∠OBD = ∠OBM
OB (гипотенуза) - общая.
Тогда ВМ = 9
АМ = 15 - 9 = 6
По теореме Пиф:
OA² = 6² + r²
OA = √(36 + r²)
AD = 12 = r + OA
r + √(36 + r²) = 12
√(36 + r²) = 12 - r
Возводим обе части в квадрат
36 + r² = 144 - 24r + r²
24r = 144 - 36
24r = 108
r = 4,5