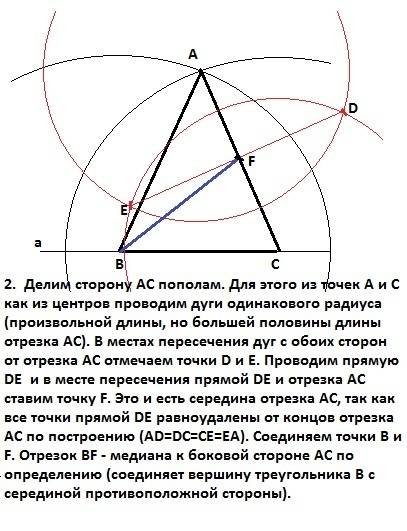
1. Строим равнобедренный треугольник. На прямой "а" откладываем произвольный отрезок (не очень большой) и обозначаем концы отрезка буквами В и С. Раствором циркуля, большим, чем длина отрезка АВ, проводим дуги. В месте пересечения этих дуг (с любой стороны от прямой "а") обозначим точку А. Соединяем точку А с точками В и С отрезками. Треугольник АВС построен, причем он равнобедренный, так как АВ=АС (радиус обеих дуг).
2. Делим сторону АС пополам. Для этого из точек А и С как из центров проводим дуги одинакового радиуса (произвольной длины, но большей половины длины отрезка АС). В местах пересечения дуг с обоих сторон от отрезка АС отмечаем точки D и Е. Проводим прямую DE и в месте пересечения прямой DE и отрезка АС ставим точку F. Это и есть середина отрезка АС, так как все точки прямой DE равноудалены от концов отрезка АС по построению (AD=DC=CE=EA). Соединяем точки В и F. Отрезок ВF - медиана к боковой стороне АС по определению (соединяет вершину треугольника В с серединой противоположной стороны).
АМ и МВ=8
МК=4
АК=АМ+МК=12см