
BC и AD лежат в разных плоскостях, не параллельны и не пересекаются. они – скрещивающиеся прямые.
Углом между скрещивающимися прямыми называется угол между двумя прямыми, параллельными им и проходящими через произвольную точку.
Рассмотрим ∆ ВАD и CAD.
АВ=АС по условию. АD - общая сторона, углы между равными сторонами равны. Следовательно. эти треугольники равны по 1-му признаку равенства треугольников. ⇒ ВD=CD и
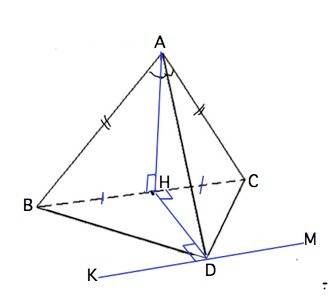
∆ ВСD- равнобедренный. Его высота DH перпендикулярна ВС и делит ВС пополам ( свойство). Н - середина ВС, ⇒ АН - высота равнобедренного ∆ АВС. Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей. ⇒ Плоскость АНD перпендикулярна плоскости АВС и DВС. Отсюда угол между АD и ВС прямой.
Или:
Проведем через вершину D прямую МК параллельно ВС.
DH перпендикулярен ВС, значит, перпендикулярен и параллельной ВС прямой МК.
АD - наклонная, HD содержит её проекцию на плоскость ВDC, По т. о 3-х перпендикулярах АD перпендикулярна МК и перпендикулярна ВС. Угол между прямыми АD и ВС равен 90°
Объяснение:
Вычисляем центр диагонали 0А по формуле
: S=(XB+XA)/2 ; (YB+YA)/2
S(OA)=(0+5)/2 ; (5+0)/2 = (5/2;5/2) = (2,5 ; 2,5)
Рассчитаем центр диагонали BО
S(BC)=(1+xB)/2 ; 3+yB)/2
* мы заменяем x и y на x и y z S(OA) (5/2;5/2)
(1+xB)/2=2,5 I *2 ; (3+yB)/2=2,5 I* 2
1+xB=5 3+yB=5
xB=5-1 yB=5-3
xB=4 yB=2
OTBET: Точка поиска B = (4; 2)
(w załączeniu grafik)