
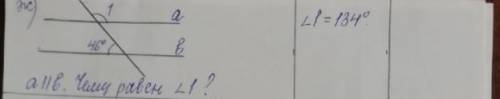

По лемме Архимеда: BST = CSA , тогда AB и CS биссектрисы углов CAS и BSA соответственно, по условию BS || AS и AB касательная к меньшей окружности, тогда TSD = ATD = CAB то есть TD || AC.
ABCS равнобедренная трапеция и AC=BC=BS = 5. (опираются на одни и те же вписанные углы)
Пусть O1 , O2 центры большей и меньших окружностей и r1, r2 их радиусы соответственно, очевидно что O1,O2,S лежат на одной прямой, из-за параллельности TD || AC то есть CAS = TDS получается CO1S = TO2S = 2*CAS , то есть треугольники TO2S , CO1S подобны, откуда ST/SC = SO2/SO1 = r2/r1 = 11/16
SC/ST = 16/11
CT/ST = 5/11
так как AT биссектриса, то по теореме о биссектрисе AC/AS = CT/ST=5/11
AC=5, AS=11
получаем равнобедренную трапецию ABCS все стороны известны
опустим высоту AH из вершины C на AS, которая равна h, тогда AH=(11-5)/2=3
CH=√(5^2-3^2) = 4
S(ABCS) = (5+11)*4/2 = 32

∠АМС = 30°
Объяснение:
Дано:
Треугольник АВС: ВС = АВ
ВМ = АС
∠АВС = 20°
Найти:
∠АМС
Cмотри прикреплённый рисунок
Сделаем дополнительные построения:
1) Cтроим параллелограмм АВТС. По свойству параллелограмма диагональ ВС делит его на два равных треугольника: ΔТСВ = ΔАВС
2) Приняв ВС за ось симметрии, построим ΔСВК симметричный ΔСВТ.
ΔСВТ = ΔСВК по построению.
При этом ∠СВК = 0,5 · (180° - 20°) =80°, ∠АВС = 20°, тогда
∠КВМ = 80° - 20° = 60°.
По условию ВМ = АС, а АС = ВТ и ВТ = ВК по построению. Тогда ВМ = ВК и ΔМВК равнобедренный. Поскольку угол при вершине В треугольника МВК равен 60°, то два угла при основании ВК равны по 60°, и ΔМВК - равносторонний.
Проекции НВ и НК сторон МВ и МК в Δ МВК являются и проекциями сторон СВ и СК равнобедренного ΔСВК. то точки Н, М и С лежат на общем перпендикуляре СН, являющимся высотой, медианой и биссектрисой обоих равнобедренных треугольников: ΔМВК и ΔСВК.
Поскольку МН - биссектриса угла КМВ. то ∠ВМН = ∠КМН = 30°.
∠АМС и ∠ВМН - вертикальные углы. поэтому ∠АМС = 30°

1 да потому что если по 2 угла в каждом треугольнике равны, то и треугольники будут равны
2 134, потому что кути смежные