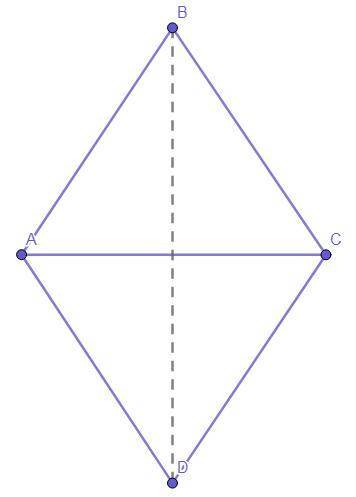
Четырёхугольник ABCD - ромб.
Отрезки АС и BD - диагонали.
АС = АВ.
Найти :Острый угол = ?
Решение :Ромб - это параллелограмм, у которого все стороны равны.
Поэтому -
АВ = ВС = CD = AD.
Рассмотрим ΔАВС.
АС = АВ = ВС.
Следовательно, ΔАВС - равносторонний (по определению равностороннего треугольника).
Каждый угол равностороннего треугольника равен по 60°.Отсюда -
∠ВАС = ∠В = ∠ВСА = 60°.
Диагональ ромба является биссектрисой его угла.То есть -
∠А = 60°*2 = 120°.
Противоположные углы параллелограмма равны.Следовательно -
∠В = ∠D = 60°
∠А = ∠С = 120°.
Отсюда острый угол ромба = 60°.
ответ :60°.
Трапеция АВСД, уголАДВ=уголВДС=30=уголДВС как внутренний разносторонний, треугольник ВСД равнобедренный, ВС=СД, уголАВД=90, уголА=90-30=60, уголА=уголД=60. трапеция равнобокая АВ=СД=ВС, треугольник АВД прямоугольный, АВ=1/2АД -лежит против угла 30,
периметр=1/2АД+1/2АД+1/2АД+АД=60, 2,5АД=60, АД=24, АВ=ВС=СД=24/2=12