правильная треугольная пирамида SABC.
R - середина ребра ВС.
S - вершина.
АВ = 7
SR = 16
Найти:S поверхности - ?
V - ?
Решение:Правильный многоугольник - многоугольник, у которого все углы и стороны равны.
Правильная пирамида - пирамида, у которой основание - правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является её высотой.
=> в основании этой правильной треугольной пирамиды лежит равносторонний △АВС.
Рассмотрим △АВС:
АВ = ВС = АС = 7, так как △АВС - равносторонний.
P△АВС = АВ + ВС + АС = 7 + 7 + 7 = 21
Так как △АВС - равносторонний => он ещё и равнобедренный.
BR = RC = 3,5, так как AR - медиана. (Также R - середина ВС, по условию)
Найдём высоту AR в △АВС, по теореме Пифагора:
с² = а² + b²
a = √c² - b²
a = √(7² - 3,5²) = √(49 - (7/2)²) = √(49 - 49/4) = √147/4 = √(147)/2 = 7√(3)/2
Итак, AR = 7√(3)/2
S осн = S △ (в основании)
S осн = S △АВС = 1/2ВС * AR = 1/2 * 7 * 7√(3)/2 = 49√(3)/4 ед.кв.
SR - высота боковой грани, так как SR - апофема.
Апофема - высота боковой грани правильной пирамиды, проведённая из её вершины.
S бок = 1/2Р * SR = 21/2 * 16 = 168 ед.кв.
S поверхности = S осн + S бок = 49√(3)/4 + 168 = 189,21762 ≈ 189 ед.кв.
Точка, на которую опущена высота SO, является серединой правильного треугольника (точка пересечения медиана).Эти медианы делятся в отношении 2:1, считая от вершины.
AR/3 - АО основания AR. (2/3)
=> AR/3 - OR основания AR (1/3)
=> OR = 1/3 * 7√(3)/2 = 7√(3)/6
Рассмотрим △SRO:
△ASO - прямоугольный, так как SO - высота.
Найдём высоту SO, по теореме Пифагора:
с² = а² + b²
a = √(c² - b²)
a = √(16² - (7√(3)/6)²) = √(256 - 49/12) = √(9069)/6
Итак SO = √(9069)/6
V = 1/3S осн * SO
V = 1/3 * 49√(3)/4 * √(9069)/6= 49√(3023)/24 ед.кб.
ответ: ≈ 189 ед.кв.; = 49√(3023)/24 ед.кб.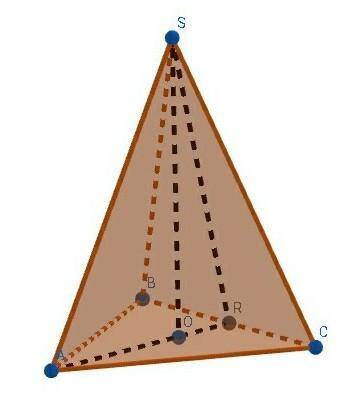
ответ: АН=9,6
Объяснение: если угол А=90°, то АМ и АТ - катеты, а МТ - гипотенуза. Найдём второй катет. Так как косинус угла- это соотношение прилежащего к углу катета к гипотенузе, то катет АМ=МТ×cosM=
=20×0,6=12
Найдём катет АТ по теореме Пифагора:
АТ²=МТ²-АМ²=20²-12²=400-144=256;
АТ=√256=16
Вычислим площадь треугольника МАТ по формуле: a×b/2,где а и b,катеты:
S=12×16/2=192/2=96.
Теперь найдём высоту АН, используя формулу площади треугольника.
S=½×а×h, где h-высота треугольника, а а- сторона, к которой проведена высота. Используем формулу обратную этой:
АН=96÷20÷½=96÷20×2=4,8×2=9,6
1) накреслить відомий катет
2) з лівого кінця провести вгору пряму перпендикулярну до цього катета (тобто під кутом 90)
3)проведем промінь бісектрису цього кута (тобто кут45)
4) відкладем задану довжину бісектриси на цьому проміні
5) зєднаемо кінці катета і бісектриси і продовжемо цей відрізок до перетину з прямою див.п2
6) отримали прямокутний трикутник, у якого один катет і бісектриса мають задану довжину