Доказательство в объяснении.
Объяснение:
Определение: внешний угол треугольника (многоугольника) - угол, образованный одной из его сторон и продолжением смежной стороны.
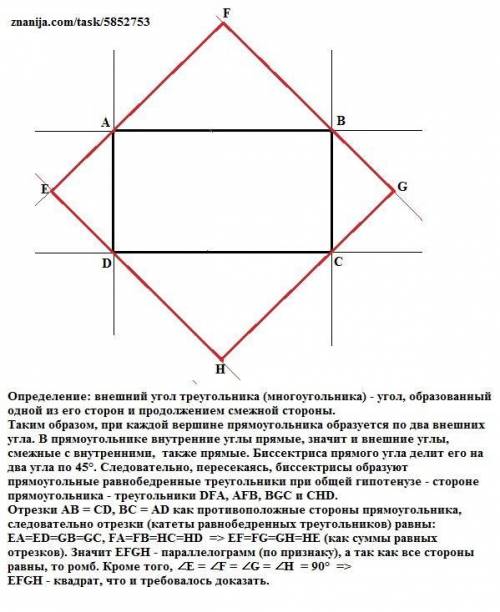
Таким образом, при каждой вершине прямоугольника образуется по два внешних угла. В прямоугольнике внутренние углы прямые, значит и внешние углы, смежные с внутренними, также прямые. Биссектриса прямого угла делит его на два угла по 45°. Следовательно, пересекаясь, биссектрисы образуют прямоугольные равнобедренные треугольники при общей гипотенузе - стороне прямоугольника - треугольники DFA, AFB, BGC и CHD.
Отрезки АВ = CD, BC = AD как противоположные стороны прямоугольника, следовательно отрезки (катеты равнобедренных треугольников) равны: EA=ED=GB=GC, FA=FB=HC=HD => EF=FG=GH=HE (как суммы равных отрезков). Значит EFGH - параллелограмм (по признаку), а так как все стороны равны, то ромб. Кроме того, ∠E = ∠F = ∠G = ∠H = 90° =>
EFGH - квадрат, что и требовалось доказать.
Средняя линия трапеции делится диагональю на отрезки, один из которых является средней линией треугольника АВС и, как средняя линия, равен половине ВС, другой - средней линией треугольника АСD и равен половине AD.
Примем КО=х, тогда ОМ=х+4
По условию КМ=10⇒
х+х+4=10 ⇒
х=3 дм.
ВС=2•КО=6 дм
АD=2•ОМ=(3+4)•2=14 дм.
Приложение
КомментарииОтметить нарушение
3
13
Мозг
Мозг
Сомневаешься в ответе?
СМОТРЕТЬ ДРУГИЕ ОТВЕТЫ
Задай вопро