В окружность вписан правильный шестиугольник со стороной 3√3. Около окружности описан правильный шестиугольник, найдите сторону этого шестиугольника.
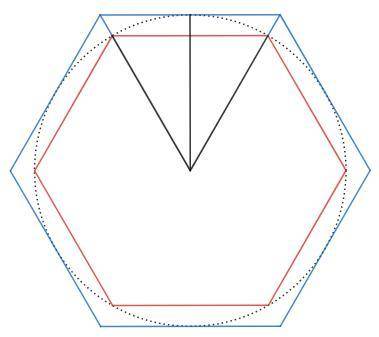
Рассмотрим вписанный шестиугольник (красный).
Проведем радиусы, угол между ними равен 1/6 полного угла, 60.
Равнобедренный треугольник с углом 60 - равносторонний.
Таким образом, радиус окружности равен стороне красного шестиугольника, 3√3.
Рассмотрим описанный шестиугольник (синий).
Соединим две вершины с центром - получим равносторонний треугольник.
Высота этого треугольника (h) - радиус вписанной окружности, 3√3.
(Радиус в точку касания перпендикулярен касательной.)
В равностороннем треугольнике
h/a =√3/2 => a =3√3 *2/√3 =6
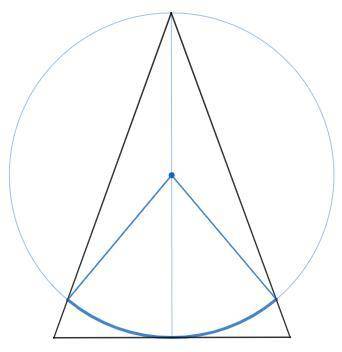
Угол при основании равнобедренного треугольника равен 70°. На высоте треугольника, проведенной к основанию и равной 27 см, как на диаметре построена окружность. Найдите длину дуги окружности, которая принадлежит треугольнику.
Длина окружности диаметром d равна пd
Длина дуги ф градусов равна пd *ф/360°
Диаметр известен, 27 см.
Найдем угол между радиусами.
Он вдвое больше угла против основания.
(Вписанный угол равен половине центрального, опирающегося на ту же дугу.)
Угол против основания 180-70*2=40
Угол искомой дуги 40*2=80
L =27п *80°/360° =6п (см)
Если -2/2 будет sin a=корень из 1-(-2/2)^2=0(здесь не уверена, посчитай еще)
Если -2 будет sin a=корень из 1-(-2)^2=-3(не знаю может быть отрицательным)
Если -3/4 посчитай по формуле той же самой)