Объяснение:
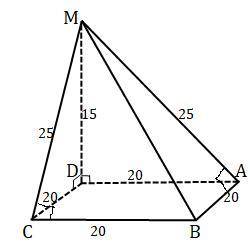
S(бок)= S(МDА)+S(МDС)+S(МАВ)+S(МСВ)
1)Т.к. МD⊥(АВС) , то МD⊥DА , МD⊥DС.
Δ МDА= МDС как прямоугольные по 2-м катетам : МD-общая, АD=DС как стороны квадрата , S(МDА)=S(МDС)=1/2*20*15=150(см²).
2) МD⊥( АВС), DА⊥АВ , значит МА⊥АВ по т. о 3-х перпендикулярах⇒ΔМАВ-прямоугольный.
МD⊥( АВС), DС⊥СВ , значит МС⊥СВ по т. о 3-х перпендикулярах⇒ΔМСВ-прямоугольный.
3) ΔМАВ= ΔМСВ, как прямоугольные по катетам МА=МС=25 и общей гипотенузе МВ. Поэтому S(МАВ)=S(МСВ)=1/2*20*25=250 (см²).
4)S(бок)= 2*150+2*250=800 (см²).
Даны векторы а(7;0;0) и b(0;0;3).Найдите множество точек М, для каждой из которых выполняется условие ОМ*а=0 и ОМ*b=0, где О-начало координат.
Векторы а(7;0;0) и b(0;0;3) заданы на осях Ox и Oz.
Скалярное произведение векторов равно нулю если они перпендикулярны.
Вектору а перпендикулярны все векторы, лежащие в плоскости yOz.
Вектору b перпендикулярны все векторы, лежащие в плоскости xOy.
ответ: множество точек М, для каждой из которых выполняется условие ОМ*а=0 это плоскость yOz.
Множество точек М, для каждой из которых выполняется условие ОМ*b=0 это плоскость xOy.