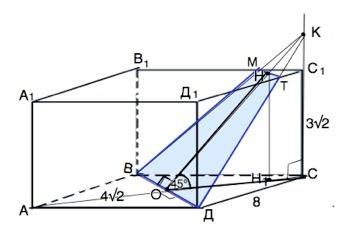
ABCD- квадрат. BD⊥AC, BD пересекает AC в точке O, АО=СО, BO=DO.
Угол 45° между плоскостью основания и плоскостью сечения - угол между отрезками, проведенными в плоскости основания и сечения перпендикулярно к диагонали BD в точке О. .
Проведем из О перпендикулярно ВD луч до пересечения в точке К с продолжением СС1.
В прямоугольном треугольнике∠КОС=45°, ⇒ угол ОКС =45° и ∆ КСО - равнобедренный .
ОС=DС•sin45°=8•√2/2=4√2
СK=ОC=4√2.
ОК=ОС:sin45°=4√2:2=8 см
Прямоугольные ∆KHC1~∆KOC по общему углу при К.
КС1=KC-CC1=4√2-3√2=√2
k=KC1/KC=√2:4√2=1/4 Тогда КН=КO•1/4,
HO=KO•3/4=8•3/4=6 см
В сечении MT||BD. Четырехугольник ВМТD- трапеция. ОН - её высота.
Диагонали квадрата - биссектрисы его углов. ABD=DBA=45°
ВD=AB:sin45°=8:√2/2=8√2
∆КМТ~∆KBD,
MT=8√2:4=2√2 см
Площадь трапеции равна произведению полусуммы оснований на высоту.
S=(MT+BD)•OH:2=((2√2+8√2)•6:2=30 см*
Объяснение:
1) Р(Δкмр) = КМ + МР + КР = 50см
Но, т.к. ΔКМР - равнобедренный, то КМ = МР, значит,
2КМ +КР = 50 (1)
2) Р(Δкме) = КМ + МЕ + КЕ = 30см, но МЕ - медиана треугольника КМР, значит, КЕ = КР/2. Тогда
Р(Δкме) = КМ + МЕ + КР/2 = 30
2КМ +2МЕ +КР = 60 → (2КМ + КР) + 2МЕ = 60
Подставляем из (1) 2КМ +КР = 50 в уравнение:
2МЕ +50 = 60
2МЕ = 10
МЕ = 10/2 = 5(см)