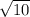Величина угла между плоскостями – угол, сторонами которого являются лучи, по которым эти плоскости пересекаются плоскостью, перпендикулярной ребру угла.
Искомый угол –это угол DHC, образованный отрезками СН и DH (см. рисунок в приложении).
СН - высота ∆ АВС, DC –⊥ плоскости ∆ АВС по условию, DH ⊥ АВ по т. о трёх перпендикулярах,
плоскость DHC перпендикулярна АВ.
СН как катет ∆ АНС, противолежащий углу 30º, равен половине гипотенузы АС и равен а/2
Тангенс угла DHC=DC/HC=[(а√3):2]:a/2=√3.
Это тангенс угла, равного 60º.
Угол между плоскостью (ADB) и плоскостью (ACB)=60º.
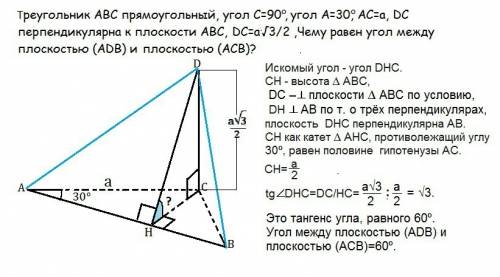
1. Прямая ВC формула прямой у=(3-х)/7
Прямая АВ формула прямой у=2х-21
Прямая АС формула прямой у= -х-3
2. у=9-3х медиана АА1
у=1/3х-39/9 - медиана ВВ1
у= -0,5х-1 - медиана СС1
3. у(АА2)=7,1х-51,5
ВВ2 высота у=х-11
СС2 уравнение у= -0,5х-1
4. А3(5;-6) т пересечения медианы АА1 и высоты ВВ2
5.tg∠A=3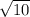
tg∠B=tg∠A
tg∠C=2/3/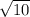
Объяснение:
1. Коэфициент при х - это (у-уо)/х т.В(10;-1)
для ВС (у-уо)/х=(-1+21)/10=2
2. АА1 - медиана Определим координаты А1(3; 0)
уравнение медианы АА1
у=9-3х
ВВ1 - медиана В1(1; -4)
у=1/3х-39/9
СС1 С1 (8; -5)
у= -0,5х-1
3.АА2 высота
А2 (7,2; -0,6)
у(АА2)=8,5/1,2х-61,8/1,2=7,1х-51,5
ВВ2 высота
координата В2=(4; -7)
у=х-11
СС2 тС2=С1 (8; -5)
у= -0,5х-1
5. tg∠A=CC1/AC1
Определяем модули векторов СС1 (12;-6) и АС1 (2;4)
tg∠A= /
/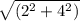 =3
=3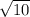
tg∠B=tg∠A
tg∠C=2*AC1/CC1=2*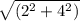 /
/ =2/3/
=2/3/