Объяснение:
Дано:
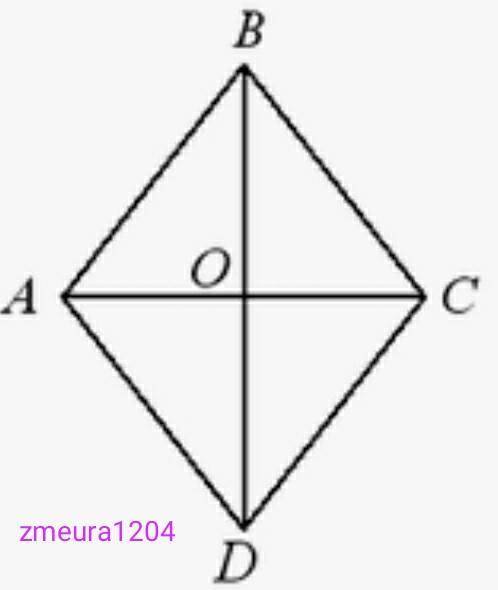
ABCD- ромб
АВ=20см
ВD=32см
АС=?
Решение
Диагонали ромба пересекаются перпендикулярно и точкой пересечения делятся пополам.
ВО=ВD:2=32:2=16см.
∆АОВ- прямоугольный треугольник.
По теореме Пифагора
АО=√(АВ²-ВО²)=√(20²-16²)=√(400-256)=
=√144=12см.
АС=2*АО=2*12=24см.
ответ: АС=24см.
2)
Дано:
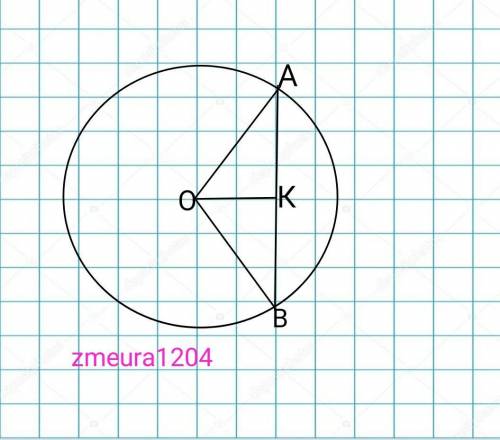
Окружность
О-центр окружности
АВ=8см хорда
ОА=ОВ=R=5см
ОК=?
Решение
ОК- высота, медиана и биссектрисса равнобедренного треугольника ∆АОВ.
ВК=КА
ВК=АВ:2=8:2=4см.
Теорема Пифагора
ОК=√(ОВ²-КВ²)=√(5²-4²)=√(25-16)=3см
ответ: 3см
Sпол=280см²
Объяснение:
S(∆ABC)=½*AB*BC=½*15*8=60см² площадь основания призмы.
∆АВС- прямоугольный треугольник
По теореме Пифагора
АС=√(АВ²+ВС²)=√(15²+8²)=√(225+64)=
=√289=17см.
Росн=АВ+ВС+АС=15+8+17=40см.
Sбок=Росн*АА1=40*4=160см²
Sпол=Sбок+2*S(∆ABC)=160+2*60=
=160+120=280см²