Объяснение:
Вариант 1
1) Треугольник существует только тогда, когда сумма любых двух его сторон больше третьей. а) нельзя, т.к. 12>8+3 б) можно
2)18>5+5 - неверно, значит 5<18+18. Основание равно 5. Р=18+18+5=41
3) 3 4
В А D-только эти точки лежат на одной прямой
7
Вариант 2
1)Треугольник существует только тогда, когда сумма любых двух его сторон больше третьей. а) может б) нельзя, т.к. 15>5+5
2)18>8+8 - неверно, значит 8<18+18. Основание равно 8. Р=18+18+8=44
3) 5 8
A B C-только эти точки лежат на одной прямой
13
Чертеж и весь счет во вложении.
Заметим, что в правильной четырехугольной пирамиде основание высоты совпадает с точкой пересечения диагоналей основания (точка О на рисунке). Следовательно, отрезок SO перпендикулярен плоскости ABC. Так как прямая AC лежит в плоскости ABC, то SO⊥AC (угол SOC прямой). Тогда SC можно найти из теоремы Пифагора для прямоугольного треугольника SOC. Нам понадобятся длины катетов SO и OC.
AC - диагональ квадрата ABCD. Значит, AC = AD*√2. OC = AC/2.
Диагональным сечением, очевидно, является треугольник SAC. Его площадь известна из условия. Зная ее и AC, находим SO.
Дальше вычисляем SC.
ответ: 10 см
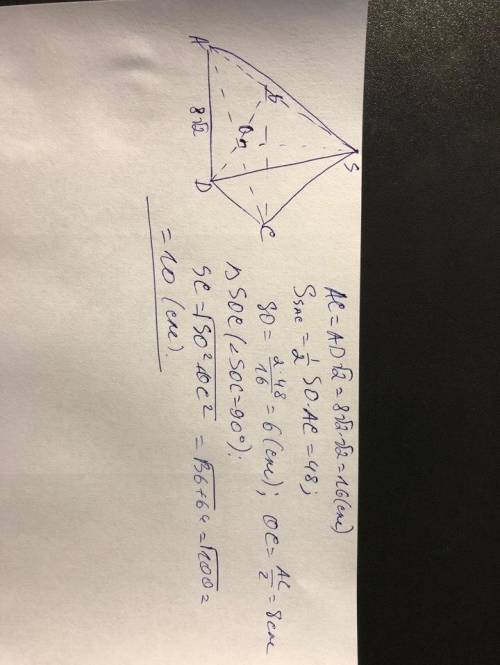
Объяснение:
1) угол АОВ центральный и равен величине дуги, на которую опирается, то есть равен величине дуги АВ,
ответ: дуга АВ(х)= 72°
2) угол х вписаный, и опирается на дугу МК, и равен половине величины этой дуги. Вся окружность 360°.
Две дуги знаем, найдем дугу МК
МК=360°-112°-46°=202°, значит угол х=202°/2=101°
ответ угол х=101°
3) получается, что ∆АОВ равносторонний, и значит все стороны равны, х=ОА=8
ответ: х=8
4) угол АВС вписаный опирается на дугу АС, и равен половине этой дуги, значит дуга АС=2*27°=54, угол АОС центральный, опирается на дугу АС и равен величине этой дуги, угол АОС=54°
ответ: угол х=54°
5) угол АОС центральный, опирается на дугу АС и равен величине этой дуги, значит дуга АС, которая меньшая равна 130°, вся окружность 360°, значит большая дуга АС=360°-130°=230°. Угол х вписаный, опирается на большую дугу АС и равен половине величины этой дуги, значит угол х=230°/2=115°
ответ: угол х=115°