12 .................
Объяснение:

Рассмотрим сечение конуса через вершину, перпендикулярное основанию.
Получится равнобедренный треугольник с углами у основания по 45 градусов и равными боковыми сторонами по 8 см.
Так как два угла треугольника-сечения известны (по 45), то можно посчитать оставшийся угол = 180 - 45 - 45 = 90. Следовательно, треугольник прямоугольный.
Диаметр (или 2 радиуса) основания конуса будет равен основанию прямоугольника (то есть неизвестной пока стороне. По совместительству, эта сторона будет являться гипотенузой.
По теореме Пифагора, гипотенуза равна корню квадратному из суммы квадратов катетов. То есть \sqrt{ 8^{2} + 8^{2} } = \sqrt {64 + 64} = \sqrt{128} = 8 \sqrt{2}
8
2
+8
2
=
64+64
=
128
=8
2
Мы нашли гипотенузу сечения, а следовательно и диаметр конуса.
Диаметр = 2 радиусам. Т.е. радиус = 4 \sqrt{2}4
2
Формула объёма конуса:
V = \frac{1}{3} \pi r^{2} hV=
3
1
πr
2
h
Осталось найти высоту.
Из вершины треугольника-сечения опустим высоту. Она попадёт прямо на середину его основания, т.е. поделит его пополам. Эта высота образует прямоугольный треугольник, где высота и радиус конуса будут катетами, а образующая конуса - гипотенузой.
Найдём по теореме Пифагора высоту:
h = \sqrt{8^{2} - (4\sqrt{2})^{2}} = \sqrt{64 - 32} = \sqrt{32} = 4 \sqrt{2}h=
8
2
−(4
2
)
2
=
64−32
=
32
=4
2
Подставляем в формулу объёма конуса всё найденное:
V = \frac{1}{3} \pi r^{2} h = \frac{ \pi * (4 \sqrt{2})^2* 4 \sqrt{2} }{3} = \frac{ \pi *128 \sqrt{2} }{3}V=
3
1
πr
2
h=
3
π∗(4
2
)
2
∗4
2
=
3
π∗128
2
Если у вас \piπ приравнивается к 3, то тройки сократятся и сотанется только 128 \sqrt{2}128
2
(см. объяснение)
Объяснение:
Поскольку пирамида правильная, то BH - медиана, биссектриса и высота треугольника ABC, то есть верно, что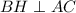 . Проведем прямую
. Проведем прямую 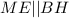 . Тогда
. Тогда 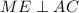 . Пусть CP другая медиана треугольника ABC. Пусть медианы этого треугольника пересекаются в точке O. Тогда из-за того, что пирамида правильная, SO - это ее высота, т.е.
. Пусть CP другая медиана треугольника ABC. Пусть медианы этого треугольника пересекаются в точке O. Тогда из-за того, что пирамида правильная, SO - это ее высота, т.е. 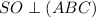 , а значит и любой прямой в этой плоскости. Пусть
, а значит и любой прямой в этой плоскости. Пусть  . Проведем через точку J прямую параллельную SO, которая пересечет SC в точке I. Тогда
. Проведем через точку J прямую параллельную SO, которая пересечет SC в точке I. Тогда 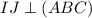 , а значит и любой прямой в этой плоскости. Соединим точки M, I и E. Получим плоскость
, а значит и любой прямой в этой плоскости. Соединим точки M, I и E. Получим плоскость 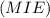 . Покажем, что
. Покажем, что 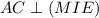 .
. 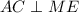 и
и 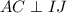 , и
, и 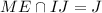 . Тогда задача сводится к нахождению площади треугольника
. Тогда задача сводится к нахождению площади треугольника 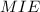 . Будем искать ее, как
. Будем искать ее, как 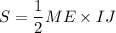 . Из подобия треугольников следует, что
. Из подобия треугольников следует, что 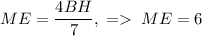 . Из подобия треугольников
. Из подобия треугольников 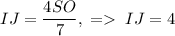 . Подставив найденное в формулу выше, получим
. Подставив найденное в формулу выше, получим 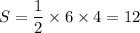 . Таким нами образом было получено, что искомая площадь равна
. Таким нами образом было получено, что искомая площадь равна 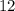 .
.
Задание выполнено!